Неизоморфные двухкомпонентные системы с простой эвтектикой. Треугольник таммана
Треугольник Таммана
Если рассматривать кривые охлаждения смесей двухкомпонентной неизоморфной системы 2, 3, 4, 6 (см. рис. 3 – I), то можно отметить, что каждая из них имеет два излома.
Первый излом указывает на появление новой фазы – это начало кристаллизации чистого компонента (для кривых охлаждения 2, 3, 4 – это начало выделения кристаллов А, для кривой охлаждения 6 – это начало выделения кристаллов В).
Второй излом, переходящий в горизонтальный отрезок, характеризует начало кристаллизации эвтектики.
На кривых охлаждения размеры этих отрезков (а, б, в, г, д) различны. Они прямо пропорционально зависят от количества выпавшей эвтектики. В нашем примере самый большой отрезок г (ЕМ) находится на кривой охлаждения 5 (состав: 30% А и 70% В), которая имеет всего один излом, переходящий в горизонтальную площадку. Это говорит о том, что мы имеем дело изначально с эвтектической смесью, чем объясняется большой размер г.
Если на диаграмме отложить отрезки (а, б, в, г, д) от линии солидуса и соединить полученные точки между собой, то образуется треугольник ТЕFM– треугольник Таммана, он позволяет рассчитать массу эвтектической смеси, которая выпадает при охлаждении системы любого состава АВ.
Пример. Пусть изначально взято 5 кг смеси состава 70% А и 30% В. Определить сколько эвтектики выделится при охлаждении данной смеси.
Решение.
Рассмотрим два треугольника. Треугольник ТЕNIIINIV подобен треугольнику ТЕЕМ, из чего вытекает
,
где ЕМ – 5кг, а отрезки ТЕЕ и ТЕNIII замеряем.
.
Вывод: при охлаждении 5 кг смеси состава 70% А и 30% В выделиться 2,22 кг эвтектической смеси.
Задача. На основании кривых охлаждения системы алюминий – кремний (рис. 4) построить диаграмму состав – температура плавления. По диаграмме определить:
При какой температуре начнется кристаллизация системы, содержащей 60% кремния?
- Какой элемент будет переходить в твердое состояние?
Какое количество твердой фазы будет образовано при охлаждении до 1000К 2 кг системы, содержащей 60% кремния?
При какой температуре кристаллизация закончится?
Определить состав последней капли жидкости.
Найти массу эвтектики при охлаждении 2 кг смеси, содержащей 60% кремния.
Решение.
На основании кривых охлаждения строим диаграмму состав – температура. При кристаллизации чистого кремния (кривая охлаждения 1) наблюдается температурная остановка при 1693К (температура плавления кремния). Эту температуру откладываем на оси температур, отвечающей чистому кремнию (L).
На кривой 2, содержащей 80% кремния, при 1593К обнаруживается уменьшение скорости охлаждения. При этом начинает выпадать чистый кремний в виде кристаллов, а жидкая фаза обогащается алюминием. При увеличении содержания алюминия, температура плавления системы уменьшается. При 845К на кривой 2 наблюдается температурная остановка (горизонтальная площадка а), после чего вся система переходит в твердое состояние. При этом одновременно выпадают в виде кристаллов и алюминий, и кремний, т.е. кристаллизуется эвтектика. Оба вида кристаллов хорошо различимы под микроскопом.
При охлаждении системы, содержащей 40% кремния (кривая 4) изменение скорости охлаждения наблюдается уже при 1219К, а горизонтальная площадка (в) наблюдается при той же температуре, что и на кривой 2 (845К), что указывает на кристаллизацию эвтектики, а так как состав эвтектики постоянен, то длина горизонтальной площадки пропорциональна количеству кристаллизующейся эвтектики.
При охлаждении системы, содержащей 10% кремния (кривая охлаждения 5) наблюдается температурная остановка при 845К. Длина горизонтальной площадки (г) максимальна на кривой 5, что означает, что система, содержащая 10% кремния, соответствует эвтектическому составу.
При охлаждении чистого алюминия (кривая 7) наблюдается температурная остановка при 932К, что соответствует температуре плавления чистого алюминия.
Закончив построение диаграммы по всем кривым охлаждения, получим две кривые ликвидуса (NE, EL) и горизонтальную прямую солидуса СЕМ, которые пересекаются в одной, так называемой эвтектической точке Е.
Выше кривых NEL (зона I) система находится в жидком состоянии.
Рис.4. Диаграмма состояния алюминий кремний
В зоне II сосуществуют кристаллы алюминия и расплав, состав которого при каждой температуре определяется по кривой NE.
В зоне III сосуществуют кристаллы кремния и расплав, состав которого определяется по кривой ЕL.
В зоне IV система находится в твердом состоянии. Так как длина горизонтальной площадки, соответствующая кристаллизации эвтектики, пропорциональна количеству эвтектики, то это можно использовать для определения массы эвтектики, которая может быть выделена из смеси любого состава. Для этого необходимо построить треугольник Таммана.
Длины горизонтальных площадок (а, б, в, г, д) откладывают вертикально вниз от СЕМ в точках, отвечающих составам смесей. Соединив нижние концы и точки С и М, получаем треугольник Таммана.
Кристаллизация смеси, содержащей 60% кремния, начнется при температуре 1421К.
В твердую фазу будет переходить кремний. Расплав будет обогащаться алюминием.
При охлаждении системы, содержащей 60% кремния до 1000К, некоторое количество кремния выделится в виде кристаллов. Для определения количества твердой и жидкой фаз применяется правило рычага.
Вес кристаллов кремния так относится к весу жидкой фазы, как отрезок OF относится к отрезку FP. Если вес системы 2 кг, то
mт + mж = 2 кг,
mж= 2 – mт.
отсюда
,
решаем уравнение относительно mт:
34 mт + 28 mт = 56,
mт = 0,903 кг.
При Т = 1000К из системы, содержащей 60% кремния, выделится кристаллического кремния.
Кристаллизация этой смеси закончится при температуре 845К – температуре эвтектики.
Состав последней капли жидкости соответствует составу эвтектики (10% кремния и 90% алюминия).
Массу эвтектики определяем из треугольника Таммана. Треугольник MKD подобен треугольнику MES, следовательно:
по условию mсистемы = 2 кг ES = 2, все отрезки замеряем,
При охлаждении 2 кг смеси, содержащей 60% кремния, выделится 0,923 кг эвтектики.
studfiles.net
Системы с полной нерастворимостью компонентов в твердом состоянии
Неизоморфные системы – это такие системы, в которых компоненты системы в жидком состоянии взаимно растворимы, а в твердом состоянии не растворимы друг в друге.
При затвердевании расплава вначале кристаллизуется один компонент, в то время как другой остается в расплаве. Поэтому в твердом состоянии такие системы неоднородны и состоят из двух твердых фаз: кристаллов компонента А и кристаллов компонента В.
Это объясняется тем, что компоненты А и В заметно отличаются структурой кристаллов. Такие смеси относят к неизоморфным. Примером таких систем могут быть Cd-Bi, Au-Tl, KCI-LiCI, CaO-MgO и т.д.
- Неизоморфные двухкомпонентные системы с простой эвтектикой
Диаграмма состояния таких систем, построенных по кривым охлаждения температура – время, выглядит так (рис. 3).
Область выше кривой СЕD – жидкий расплав, характеризуется тем, что в известных пределах можно менять температуру и состав независимо друг от друга, не вызывая появления новых фаз.
Поле Ж принадлежит однофазной системе, следовательно, число степеней свободы () равно 2. Система двухвариантна (бивариантна).
Рис. 3. Построение диаграммы состояния двухкомпонентной неизоморфной системы с простой эвтектикой:
I– кривые охлаждения;
II– диаграмма состояния;
III– кривая охлаждения фигуративной т.N
Точки С и D изображают температуры кристаллизации чистых компонентов (соответственно компонента А и компонента В). При этих температурах система инвариантна (). При температурах выше С или D соответственно чистые компоненты находятся в расплаве (), система моновариантна и при температурах ниже С и D в твердом состоянии (), система тоже моновариантна.
Поле Ж ограничивается кривой СЕD, которая отвечает предельно охлажденной жидкой фазе и называется линией ликвидуса (лат. liquor – жидкость).
Фигуративные точки 1 двух ветвей ликвидуса (СЕ и ЕD) характеризуют температуры, при которых из жидких расплавов начинается кристаллизация соответственно компонента А или В, и одновременно фигуративные точки на ветвях ликвидуса характеризуют состав жидких расплавов, при охлаждении которых начинается кристаллизация одного из компонентов.
Как уже упоминалось линия ликвидуса состоит из 2-х ветвей СЕ и ЕD, сходящихся в точке Е. Это значит, что каждой ветви ликвидуса соответствует своя твердая фаза, равновесная с жидким расплавом, а излом в точке Е связан с появлением новой фазы.
Опыт показывает, что ветвь ликвидуса СЕ соответствует началу кристаллизации компонента А соответствующих расплавов, а фигуративные точки кривой ЕD – началу выделения из расплава кристаллов В.
Кристаллизация одного из компонентов вызывает повышение содержания другого компонента в расплаве, что приводит к понижению температуры кристаллизации. Когда она станет наименьшей и равной отрезку СТЕ, то расплав насыщается в отношении обоих компонентов, тогда и происходит их совместная кристаллизация с появлением новой твердой фазы, что отображается на кривой ликвидуса изломом в точку Е.
Наименьшая постоянная температура, при которой кристаллизуются оба компонента, называется эвтектической температурой. При этой температуре находятся 3 фазы: жидкий расплав, кристаллы А и кристаллы В, т.е. , система безвариантна. Поэтому строго постоянное значение имеет не только температура, но и состав жидкой фазы.
Смесь компонентов, кристаллизующихся без изменения состава жидкой фазы, называется эвтектической смесью или просто эвтектикой (от греч. eutektik – легко плавящийся).
Последняя не меняется по составу до конца кристаллизации. Таким образом, при охлаждении эвтектической смеси кристаллизация происходит без изменения состава (состав жидкой фазы одинаков) до тех пор, пока вся система не закристаллизуется. Т.е. данная смесь ведет себя как однокомпонентная, и на кривой охлаждения этот фазовый переход характеризуется горизонтальной площадкой.
Поля СЕТЕ и DEF состоят из двух фаз (ж + кр1А и ж + кр В), в которых соответственно кристаллы А и кристаллы В находятся в равновесии с расплавом. Концентрация расплава при каждой температуре находится на пересечении изотермической линии, называемой нодой, с соответствующей ветвью ликвидуса.
Рассмотрим процесс охлаждения расплава, заданного фигуративной точкой N.
На диаграмме в точке N имеем двухвариантную систему. , тогда
т.е. можно менять произвольно температуру и состав (в разумных пределах) без изменения числа и вида фаз. При температуре Т2 (NI) начинается выпадение кристаллов вещества А – появляется твердая фаза, т.е. , тогда, система становится моновариантной. Это значит, что можно менять только температуру, а состав расплава при каждой температуре будет определяться кривойСЕ.
При дальнейшем охлаждении системы продолжается понижение температуры и выпадение кристаллов вещества А из расплава. В результате расплав обогащается компонентом В. В точке NII система продолжает оставаться моновариантной. Для определения состава расплава через точку NII проведем горизонтальную линию – ноду Т3NIIO. По точкам Т3 и О определим температуру Т3 и состав расплава (жидкой фазы), спроектировав точку О на ось состава (nI).
Кроме температуры и состава полученная диаграмма позволяет определить количественные соотношения между твердой и жидкой фазой, которые описываются правилом рычага.
| Отношение количеств равновесных фаз обратно пропорционально отношению отрезков, отсекаемых на ноде точкой общего состава системы. |
Для нашего случая .
Пример. 10 кг смеси состава n охлаждают до температуры Т3. Определить массу выпавших кристаллов А.
Решение.
Дана общая масса системы (10 кг), следовательно, . Согласно правилу рычагазамеряем отрезкиNIIO и Т3NII и получаем решаем уравнение 33m т = 130 m т = 3,94 кг.
Вывод: при охлаждении 10 кг смеси состава n до температуры Т3 выделится 3,94 кг кристаллов А.
В точке NIII начинают выпадать первые кристаллы вещества В, следовательно, в системе находятся 3 фазы: одна жидкая (расплав состава nЕ) и две твердые (кристаллы А и кристаллы В), т.е. , тогда, система безвариантна. Значениепоказывает, что эти три фазы могут находиться в равновесии только при вполне определенных условиях, когда температура равна эвтектической температуре (ТЕ), а раствор имеет эвтектический состав (nЕ). Ни температуру, ни состав невозможно в этом случае изменить, не изменив число и вид фаз. Согласно закону фазового равновесия Гиббса, кристаллизация эвтектики из раствора должна происходить при постоянной температуре, кроме того, соотношение масс кристаллов А и В в выпавшей эвтектике должно быть таким же, как и массовое содержание веществ А и В в расплаве эвтектического состава.
В связи с тем, что кристаллы А и В при кристаллизации эвтектики выпадают одновременно и у них нет условий для роста кристаллов, твердая эвтектика имеет мелкокристаллическую структуру. Застывший расплав состава NIII(ниже температуры ТЕ) состоит из сравнительно крупных кристаллов А, которые выпали в интервале температур между точками NI и NIII и мелкокристаллической смеси кристаллов А и В твердой эвтектической смеси.
Процесс кристаллизации заканчивается в фигуративной точке NIII при температуре ТЕ полным застыванием жидкого раствора (расплава).
После исчезновения жидкой фазы в системе остаются только две фазы: кристаллы А и кристаллы В. Это значит, что произвольно может меняться только температура.
В точке NIV продолжается охлаждение двух твердых фаз.
Кривая охлаждения для рассмотренного случая будет выглядеть так (см. рис. 3 III).
Участок N – NI: ,, охлаждение идет равномерно по закону Ньютона.
Участок NI-NII: в т. NI наблюдается излом, что говорит о появлении новой фазы – начинает кристаллизоваться вещество А. Кривая охлаждения опускается более полого, чем на участке N – NI. Это объясняется тем, что при кристаллизации вещества А из расплава выделяется теплота, которая замедляет педение температуры, следовательно, ,.
При дальнейшем охлаждении температура понижается до эвтектической температуры ТЕ, система достигает фигуративной точки NIII, при этом состав жидкой фазы в точке Е становится эвтектическим и начинается выпадение твердой эвтектики, т.е. смеси кристаллов А и В. (крА + кр В + Ж), следовательно .NIII – начало кристаллизации эвтектики, NIV – конец кристаллизации эвтектики.
studfiles.net
Содержание
ВВЕДЕНИЕ…………………………………………………..…5
ФАЗОВЫЕ ДИАГРАММЫ……………………………………6
Работа 1 Физико-химический анализ двухкомпонентной смеси…………………………………………………………..……11
Работа 2 Термический анализ лекарственных смесей………………………………………………...…………..…16
Работа 3 Изучение взаимной растворимости трехкомпонентной системы…………………………………………………………...20
СВОЙСТВА РАЗБАВЛЕННЫХ РАСТВОРОВ.…………….24
Работа 4 Определение изотонического коэффициента i электролита в водномрастворе методом криоскопии……………...........................................................................26
ЭЛЕКТРОПРОВОДНОСТЬ РАСТВОРОВ ЭЛЕКТРОЛИТОВ…………………………………………………………...…30
Работа 5 Определение электропроводности и константы диссоциации слабогоэлектролита………………………………………………………………..35
Работа 6 Кондуктометрическое титрование……………….…38
ЭЛЕКТРОДНЫЕ ПОТЕНЦИАЛЫ И ЭЛЕКТРОДВИЖУЩИЕ СИЛЫ…………………...…………………………..….42
Работа 7 Измерение ЭДС гальванического элемента…………………………………………………….………….51
Работа 8 Измерение окислительно-восстановительных потенциалов………………………………………………………..……..56
АДСОРБЦИЯ…………………………………………….…...59
Работа 9 Влияние различных факторов на величину адсорбции из растворов…………………………………………………….66
Работа 10 Изучение адсорбции поверхностно-активного вещества (ПАВ) награнице воздух-раствор……………………...68
Работа 11 Исследование поверхностной активности ПАВ одного гомологического ряда…………………………….......……75
ГАЗОВАЯ ХРОМОТОГФИЯ…………………….…………....77
Работа 12 Качественный и количественный анализ углеводородов с помощьюгазовой хроматографии…...…………………………………………………………84
ХИМИЧЕСКАЯ КИНЕТИКА……………………………..…91
Работа 13 Изучение кинетики гомогенного каталитического разложения Н2О2…………………………………………………...95
Работа 15 Определение константы скорости инверсии сахарозы…………………………………………………...…………108
ПРИЛОЖЕНИЕ..............................................................................115
ВВЕДЕНИЕ
Практикум по физической и коллоидной химии (ч.1) предназначен для студентов медицинского факультета специальности "Фармация" и включает 15 работ.
Лабораторные работы выполняются параллельно с изучением теоретического курса. Каждая работа представляет собой небольшое исследование, при проведении которого студенты получают навыки экспериментальной работы, овладевают методами физико-химических измерений, получивших широкое применение в фармации, учатся анализировать полученные экспериментальные данные и на основе этого делать обобщающие выводы.
Для выполнения каждой лабораторной работы необходимо:
Изучить по конспекту лекций и учебнику теоретический материал, необходимый для выполнения работы;
Внимательно прочитать описание лабораторной работы и ответить на вопросы в конце описания;
Выполнить опыт и в лабораторном журнале оформить отчет. В отчете указывается название лабораторной работы, ее цель, записываются основные уравнения и вычисления. Результаты опытов оформляются в виде таблиц и графиков на миллиметровой бумаге. Запрещается вести запись лабораторных работ на отдельных листочках и в черновых тетрадях. В заключении каждого отчета формулируются основные выводы.
Защитить лабораторную работу у преподавателя.
ФАЗОВЫЕ ДИАГРАММЫ
Фазовые диаграммы показывают зависимость состава многокомпонентных систем от внешних факторов (температуры, давления) и описывают происходящие в системах фазовые превращения. Эти диаграммы позволяют делать выводы о составе смеси веществ, их взаимодействии (образовании новых химических соединений и растворов), а также границах их существования.
Знание фазовых диаграмм используется в фармацевтическом анализе для идентификации и определения чистоты лекарственных препаратов, выбора наиболее оптимальных путей их выделения из смесей, определения состава смесей для решения вопроса о совместимости лекарственных препаратов.
Фазовые диаграммы "состав системы - температура" (диаграммы плавкости) строят на основании кривых охлаждения - зависимости температуры системы от времени ее охлаждения. Число компонентов К и число фаз в системе Ф связаны правилом фаз Гиббса, которое при постоянном давлении выражается уравнением:
С = К - Ф + 1 (1.1),
где С - число степеней свободы, показывающее количество параметров (число компонентов и температуру), которые можно менять при сохранении заданного числа фаз.
Однокомпонентные системы
На рис.1.1 представлены кривые охлаждения для чистого вещества (К=1).
время
Рис. 1.1 Кривые охлаждения однокомпонентной системы.
Участок ab кривой 1 соответствует охлаждению жидкого вещества (Ф=1),что соответствует степени свободы С=1, и температура системы непрерывно уменьшается. При температуре кристаллизации tk в точке “b” появляются первые кристаллы и система становится двухфазной (Ф=2). При этом на кривой охлаждения наблюдается излом.
На участке bс число степеней свободы равно нулю (С=0), и температура в процессе кристаллизации не изменяется (горизонтальный участок площадки на кривой охлаждения). Потери тепла системой компенсируются теплотой выделяющейся при кристаллизации. В точке “с” исчезают последние капли жидкости и на участке cd происходит охлаждение твердого вещества , при этом С=1.
Однако на практике жидкость может переохладиться до температуры ниже tk. В этом случае на участке bс кривой 2 образования кристаллов не наблюдается, хотя температура ниже температуры кристаллизации, но после формирования первых кристаллов выделение теплоты кристаллизации приводит к повышению температуры до
tк (участок сd кривой 2). В точке “е” кристаллизация заканчивается и на участке ef происходит охлаждение кристаллов С=1.
Двухкомпонентные системы
Рассмотрим систему из двух веществ А и В (К=2), температуры кристаллизации (плавления) которых tА и tВ. Если не происходит переохлаждения, то для чистого вещества А кривая охлаждения (кривая А рис. 1.2) имеет горизонтальную площадку при температуре tА.
D
F
Рис. 1.2 Кривые охлаждения (а) и диаграмма плавкости и треугольник Таммана (б) двухкомпонентной системы.
Для смеси А и В состава x1 температура начала кристаллизации вещества А t1 ниже температуры ta.На кривой охлаждения (рис. 1.2) системы состава x1 началу кристаллизации вещества А соответствует излом при температуре t1. В процессе кристаллизации компонента А его концентрация в жидкости уменьшается, а концентрация В увеличивается, что и приводит к постепенному понижению температуры кристаллизации А вплоть до tэ. По правилу фаз в ходе кристаллизации вещества А из раствора система, содержащая 2 компонентп и 2 фазы, имеет одну степень свободы (С=2-2+1=1), поэтому температура кристаллизации изменяется. Снижение скорости охлаждения системы при температурах ниже t1 связано с выделением в системе теплоты кристаллизации. При температуре tэ жидкий раствор становится насыщенным в отношении вещества В, которое при этих условиях также начинает кристаллизоваться. Система становится трехфазной (жидкость, кристаллы и кристаллы В), и число ее степеней свободы равно нулю (С=2-3+1=0). Таким образом, одновременная кристаллизация А и В из раствора происходит при постоянных температуре (tэ) и составе жидкого раствора (xэ).Эта температура называется эвтектической. На кривой охлаждения 1(рис.1.2) процессу одновременной кристаллизации А и В соответствует площадка при tэ. Расплав, из которого одновременно выпадают кристаллы А и В, называется эвтектическим расплавом, образующаяся при этом смесь мелких кристаллов двух веществ называется эвтектикой. Ниже tэ , система содержит две фазы (кристаллыА и кристаллыB) и число степенейсвободы равно 1 (C=2-2+1=1).
Для смеси состава x2 (кривая 2 (рис. 1.2)), содержащей больше веществ В, чем смесь x1,кристаллизация А начинается, в соответствии со сказаннымранее, при более низкой температуреt2. Когда выпадение кристалловА приведёт к такой концентрации вещества В, что оно также начнёт кристаллизоваться, то температура одновременной кристаллизацииAиВбудет такой же, как и для смеси 1. Если же взять смесь xэ, состав которой позволяет веществам А и В кристаллизоваться одновременно без предварительного выпадения кристаллов А или кристаллов В, то криваяохлаждения будет изображаться как кривая 3(охлаждение расплава эвтектического состава). Для смесиx4, содержащейизбыток вещества В по сравнению с концентрацией xэ , кривая охлаждения подобна кривой 2, но сначала выпадают кристаллы В, и только при достижении состава раствора, допускающего одновременную кристаллизациюА иВ, наблюдается горизонтальная площадка при температуреtэ .
Чем ближе по составу расплав к эвтектике, тем длиннее горизонтальные участки на кривых охлаждения, так как масса эвтектики увеличивается.
Диаграмма состояния двухкомпонентной системы в координатах температура-состав (рис. 1.2,б) строится на основании кривых охлаждения и называется диаграммой плавкости. Например, для чистого вещества А (левая ось ординат диаграммы плавкости) температура кристаллизации tА, для смеси x1, содержащей 20% вещества В, кристаллизация начинается при температуреt1, что на диаграмме соответствует точке 1. Для смесей x2,xЭ иx4 начало кристаллизации показано точками 2, 3 и 4. Следовательно, область диаграммы над линиейtА3 иtB3 соответствует жидкому состоянию системы.Такие линии называют линиями ликвидуса от латинского слова liquidus (жидкость), и область диаграммы над ней обозначают буквойL.Твёрдое тело по латыни называется solidus, поэтому существование твердой фазы в области диаграммы обозначают буквой S.
Области диаграммы между кривой ta3,tb3 и прямой tЭD отвечают двухфазным (гетерогенным) состояниям системы, так как в ней при этихусловиях присутствуют жидкость и кристаллы веществ А или В. Как видно из диаграммы( рис. 1.2.б) есть две области L + S: в левой - жидкая фаза находится в равновесии с кристаллами веществаA (L + SА), а в правой - с кристаллами веществаВ(L + SВ). Область диаграммы под прямой tЭDсоответствует двум твёрдым фазам и обозначается как (SА + SВ), потому что система в данном случае состоит из смеси кристалловАиВ. Система из трех фаз может существовать только при температуреtЭ (линия tЭD).
Если на диаграмме отложить по вертикали вниз отрезки, пропорциональные или равные длинам горизонтальных участков(площадок) от оси состава для всех исследованных смесей, и соединить их концы, то можно получить треугольник Таммана(∆ABF). Причем максимальную эвтектическую площадку имеет смесь эвтектического состава. Этот треугольник позволяет экстраполяцией определить эвтектический состав, если он не попал в составы исследуемых смесей.
Таким образом, получив из опыта кривые охлаждения ряда смесей с известным соотношением двух данных компонентов, можно построить диаграмму плавкости.
studfiles.net
Неизоморфные двухкомпонентные системы с простой эвтектикой
⇐ ПредыдущаяСтр 4 из 7Следующая ⇒Диаграмма состояния таких систем, построенных по кривым охлаждения температура – время, выглядит так (рис. 3).
Область выше кривой СЕD – жидкий расплав, характеризуется тем, что в известных пределах можно менять температуру и состав независимо друг от друга, не вызывая появления новых фаз.
Поле Ж принадлежит однофазной системе, следовательно, число степеней свободы ( 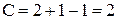 ) равно 2. Система двухвариантна (бивариантна).
) равно 2. Система двухвариантна (бивариантна).
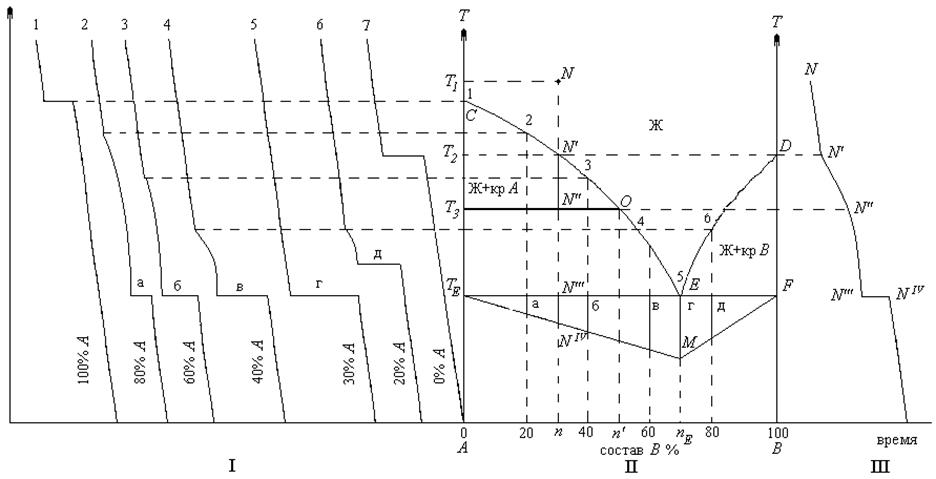
Рис. 3. Построение диаграммы состояния двухкомпонентной неизоморфной системы с простой эвтектикой:
I – кривые охлаждения;
II – диаграмма состояния;
III – кривая охлаждения фигуративной т. N
Точки С и D изображают температуры кристаллизации чистых компонентов (соответственно компонента А и компонента В). При этих температурах система инвариантна ( 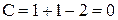 ). При температурах выше С или D соответственно чистые компоненты находятся в расплаве (
). При температурах выше С или D соответственно чистые компоненты находятся в расплаве ( 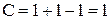 ), система моновариантна и при температурах ниже С и D в твердом состоянии (
), система моновариантна и при температурах ниже С и D в твердом состоянии ( 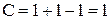 ), система тоже моновариантна.
), система тоже моновариантна.
Поле Ж ограничивается кривой СЕD, которая отвечает предельно охлажденной жидкой фазе и называется линией ликвидуса (лат. liquor – жидкость).
Фигуративные точки [1] двух ветвей ликвидуса (СЕ и ЕD) характеризуют температуры, при которых из жидких расплавов начинается кристаллизация соответственно компонента А или В, и одновременно фигуративные точки на ветвях ликвидуса характеризуют состав жидких расплавов, при охлаждении которых начинается кристаллизация одного из компонентов.
Как уже упоминалось линия ликвидуса состоит из 2-х ветвей СЕ и ЕD, сходящихся в точке Е. Это значит, что каждой ветви ликвидуса соответствует своя твердая фаза, равновесная с жидким расплавом, а излом в точке Е связан с появлением новой фазы.
Опыт показывает, что ветвь ликвидуса СЕ соответствует началу кристаллизации компонента А соответствующих расплавов, а фигуративные точки кривой ЕD – началу выделения из расплава кристаллов В.
Кристаллизация одного из компонентов вызывает повышение содержания другого компонента в расплаве, что приводит к понижению температуры кристаллизации. Когда она станет наименьшей и равной отрезку СТЕ, то расплав насыщается в отношении обоих компонентов, тогда и происходит их совместная кристаллизация с появлением новой твердой фазы, что отображается на кривой ликвидуса изломом в точку Е.
Наименьшая постоянная температура, при которой кристаллизуются оба компонента, называется эвтектической температурой. При этой температуре находятся 3 фазы: жидкий расплав, кристаллы А и кристаллы В, т.е. 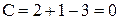 , система безвариантна. Поэтому строго постоянное значение имеет не только температура, но и состав жидкой фазы.
, система безвариантна. Поэтому строго постоянное значение имеет не только температура, но и состав жидкой фазы.
Смесь компонентов, кристаллизующихся без изменения состава жидкой фазы, называется эвтектической смесью или просто эвтектикой(от греч. eutektik – легко плавящийся).
Последняя не меняется по составу до конца кристаллизации. Таким образом, при охлаждении эвтектической смеси кристаллизация происходит без изменения состава (состав жидкой фазы одинаков) до тех пор, пока вся система не закристаллизуется. Т.е. данная смесь ведет себя как однокомпонентная, и на кривой охлаждения этот фазовый переход характеризуется горизонтальной площадкой.
Линия ТЕЕF – предельно нагретый твердый раствор называется линией солидуса(solid – твердый). Каждая точка на прямой ТЕЕF показывает состав системы, состоящей из расплава (точка Е) и двух твердых фаз: кристаллов А и кристаллов В. Ниже линии солидуса (ТЕЕF) жидкая фаза отсутствует.
Поля СЕТЕ и DEF состоят из двух фаз (ж + кр[2] А и ж + кр В), в которых соответственно кристаллы А и кристаллы В находятся в равновесии с расплавом. Концентрация расплава при каждой температуре находится на пересечении изотермической линии, называемой нодой, с соответствующей ветвью ликвидуса.
Рассмотрим процесс охлаждения расплава, заданного фигуративной точкой N.
На диаграмме в точке N имеем двухвариантную систему. 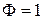 , тогда
, тогда
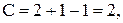
т.е. можно менять произвольно температуру и состав (в разумных пределах) без изменения числа и вида фаз. При температуре Т2 (NI) начинается выпадение кристаллов вещества А – появляется твердая фаза, т.е. 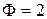 , тогда
, тогда 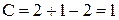 , система становится моновариантной. Это значит, что можно менять только температуру, а состав расплава при каждой температуре будет определяться кривой СЕ.
, система становится моновариантной. Это значит, что можно менять только температуру, а состав расплава при каждой температуре будет определяться кривой СЕ.
При дальнейшем охлаждении системы продолжается понижение температуры и выпадение кристаллов вещества А из расплава. В результате расплав обогащается компонентом В. В точке NII система продолжает оставаться моновариантной. Для определения состава расплава через точку NII проведем горизонтальную линию – ноду Т3NIIO. По точкам Т3 и О определим температуру Т3 и состав расплава (жидкой фазы), спроектировав точку О на ось состава (nI).
Кроме температуры и состава полученная диаграмма позволяет определить количественные соотношения между твердой и жидкой фазой, которые описываются правилом рычага.
| Отношение количеств равновесных фаз обратно пропорционально отношению отрезков, отсекаемых на ноде точкой общего состава системы. |
Для нашего случая 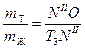 .
.
Пример. 10 кг смеси состава n охлаждают до температуры Т3. Определить массу выпавших кристаллов А.
Решение.
Дана общая масса системы (10 кг), следовательно, 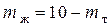 . Согласно правилу рычага
. Согласно правилу рычага 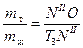 замеряем отрезки NIIO и Т3NII и получаем
замеряем отрезки NIIO и Т3NII и получаем 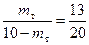 решаем уравнение 33 m т = 130 Þ m т = 3,94 кг.
решаем уравнение 33 m т = 130 Þ m т = 3,94 кг.
Вывод: при охлаждении 10 кг смеси состава n до температуры Т3 выделится 3,94 кг кристаллов А.
В точке NIII начинают выпадать первые кристаллы вещества В, следовательно, в системе находятся 3 фазы: одна жидкая (расплав состава nЕ) и две твердые (кристаллы А и кристаллы В), т.е. 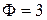 , тогда
, тогда 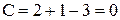 , система безвариантна. Значение
, система безвариантна. Значение 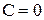 показывает, что эти три фазы могут находиться в равновесии только при вполне определенных условиях, когда температура равна эвтектической температуре (ТЕ), а раствор имеет эвтектический состав (nЕ). Ни температуру, ни состав невозможно в этом случае изменить, не изменив число и вид фаз. Согласно закону фазового равновесия Гиббса, кристаллизация эвтектики из раствора должна происходить при постоянной температуре, кроме того, соотношение масс кристаллов А и В в выпавшей эвтектике должно быть таким же, как и массовое содержание веществ А и В в расплаве эвтектического состава.
показывает, что эти три фазы могут находиться в равновесии только при вполне определенных условиях, когда температура равна эвтектической температуре (ТЕ), а раствор имеет эвтектический состав (nЕ). Ни температуру, ни состав невозможно в этом случае изменить, не изменив число и вид фаз. Согласно закону фазового равновесия Гиббса, кристаллизация эвтектики из раствора должна происходить при постоянной температуре, кроме того, соотношение масс кристаллов А и В в выпавшей эвтектике должно быть таким же, как и массовое содержание веществ А и В в расплаве эвтектического состава.
В связи с тем, что кристаллы А и В при кристаллизации эвтектики выпадают одновременно и у них нет условий для роста кристаллов, твердая эвтектика имеет мелкокристаллическую структуру. Застывший расплав состава NIII (ниже температуры ТЕ) состоит из сравнительно крупных кристаллов А, которые выпали в интервале температур между точками NI и NIII и мелкокристаллической смеси кристаллов А и В твердой эвтектической смеси.
Процесс кристаллизации заканчивается в фигуративной точке NIII при температуре ТЕ полным застыванием жидкого раствора (расплава).
После исчезновения жидкой фазы в системе остаются только две фазы: кристаллы А и кристаллы В. Это значит, что произвольно может меняться только температура.
В точке NIV продолжается охлаждение двух твердых фаз.
Кривая охлаждения для рассмотренного случая будет выглядеть так (см. рис. 3 - III).
Участок N – NI: 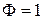 ,
, 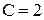 , охлаждение идет равномерно по закону Ньютона.
, охлаждение идет равномерно по закону Ньютона.
Участок NI-NII: в т. NI наблюдается излом, что говорит о появлении новой фазы – начинает кристаллизоваться вещество А. Кривая охлаждения опускается более полого, чем на участке N – NI. Это объясняется тем, что при кристаллизации вещества А из расплава выделяется теплота, которая замедляет педение температуры, следовательно, 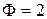 ,
, 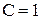 .
.
При дальнейшем охлаждении температура понижается до эвтектической температуры ТЕ, система достигает фигуративной точки NIII, при этом состав жидкой фазы в точке Е становится эвтектическим и начинается выпадение твердой эвтектики, т.е. смеси кристаллов А и В. 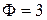 (кр А + кр В + Ж), следовательно
(кр А + кр В + Ж), следовательно 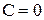 . NIII – начало кристаллизации эвтектики, NIV – конец кристаллизации эвтектики.
. NIII – начало кристаллизации эвтектики, NIV – конец кристаллизации эвтектики.
Треугольник Таммана
Если рассматривать кривые охлаждения смесей двухкомпонентной неизоморфной системы 2, 3, 4, 6 (см. рис. 3 – I), то можно отметить, что каждая из них имеет два излома.
Первый излом указывает на появление новой фазы – это начало кристаллизации чистого компонента (для кривых охлаждения 2, 3, 4 – это начало выделения кристаллов А, для кривой охлаждения 6 – это начало выделения кристаллов В).
Второй излом, переходящий в горизонтальный отрезок, характеризует начало кристаллизации эвтектики.
На кривых охлаждения размеры этих отрезков (а, б, в, г, д) различны. Они прямо пропорционально зависят от количества выпавшей эвтектики. В нашем примере самый большой отрезок г (ЕМ) находится на кривой охлаждения 5 (состав: 30% А и 70% В), которая имеет всего один излом, переходящий в горизонтальную площадку. Это говорит о том, что мы имеем дело изначально с эвтектической смесью, чем объясняется большой размер г.
Если на диаграмме отложить отрезки (а, б, в, г, д) от линии солидуса и соединить полученные точки между собой, то образуется треугольник ТЕFM– треугольник Таммана, он позволяет рассчитать массу эвтектической смеси, которая выпадает при охлаждении системы любого состава АВ.
Пример. Пусть изначально взято 5 кг смеси состава 70% А и 30% В. Определить сколько эвтектики выделится при охлаждении данной смеси.
Решение.
Рассмотрим два треугольника. Треугольник ТЕNIIINIV подобен треугольнику ТЕЕМ, из чего вытекает
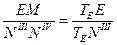 ,
,
где ЕМ – 5кг, а отрезки ТЕЕ и ТЕNIII замеряем.
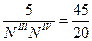
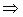
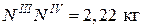 .
.
Вывод: при охлаждении 5 кг смеси состава 70% А и 30% В выделиться 2,22 кг эвтектической смеси.
Задача. На основании кривых охлаждения системы алюминий – кремний (рис. 4) построить диаграмму состав – температура плавления. По диаграмме определить:
1. При какой температуре начнется кристаллизация системы, содержащей 60% кремния?
2. Какой элемент будет переходить в твердое состояние?
3. Какое количество твердой фазы будет образовано при охлаждении до 1000К 2 кг системы, содержащей 60% кремния?
4. При какой температуре кристаллизация закончится?
5. Определить состав последней капли жидкости.
6. Найти массу эвтектики при охлаждении 2 кг смеси, содержащей 60% кремния.
Решение.
На основании кривых охлаждения строим диаграмму состав – температура. При кристаллизации чистого кремния (кривая охлаждения 1) наблюдается температурная остановка при 1693К (температура плавления кремния). Эту температуру откладываем на оси температур, отвечающей чистому кремнию (L).
На кривой 2, содержащей 80% кремния, при 1593К обнаруживается уменьшение скорости охлаждения. При этом начинает выпадать чистый кремний в виде кристаллов, а жидкая фаза обогащается алюминием. При увеличении содержания алюминия, температура плавления системы уменьшается. При 845К на кривой 2 наблюдается температурная остановка (горизонтальная площадка - а), после чего вся система переходит в твердое состояние. При этом одновременно выпадают в виде кристаллов и алюминий, и кремний, т.е. кристаллизуется эвтектика. Оба вида кристаллов хорошо различимы под микроскопом.
При охлаждении системы, содержащей 40% кремния (кривая 4) изменение скорости охлаждения наблюдается уже при 1219К, а горизонтальная площадка (в) наблюдается при той же температуре, что и на кривой 2 (845К), что указывает на кристаллизацию эвтектики, а так как состав эвтектики постоянен, то длина горизонтальной площадки пропорциональна количеству кристаллизующейся эвтектики.
При охлаждении системы, содержащей 10% кремния (кривая охлаждения 5) наблюдается температурная остановка при 845К. Длина горизонтальной площадки (г) максимальна на кривой 5, что означает, что система, содержащая 10% кремния, соответствует эвтектическому составу.
При охлаждении чистого алюминия (кривая 7) наблюдается температурная остановка при 932К, что соответствует температуре плавления чистого алюминия.
Закончив построение диаграммы по всем кривым охлаждения, получим две кривые ликвидуса (NE, EL) и горизонтальную прямую солидуса СЕМ, которые пересекаются в одной, так называемой эвтектической точке Е.
Выше кривых NEL (зона I) система находится в жидком состоянии.
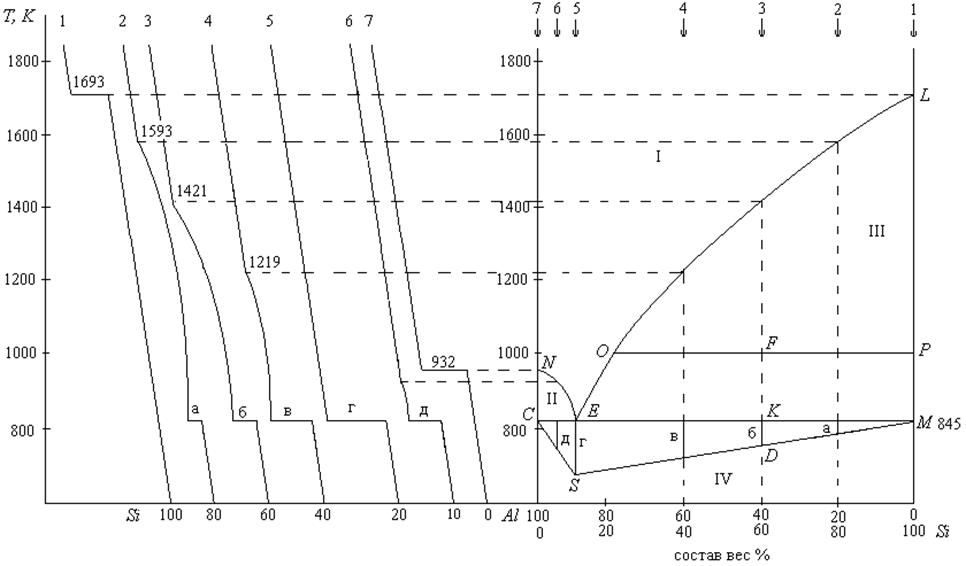
Рис.4. Диаграмма состояния алюминий - кремний
В зоне II сосуществуют кристаллы алюминия и расплав, состав которого при каждой температуре определяется по кривой NE.
В зоне III сосуществуют кристаллы кремния и расплав, состав которого определяется по кривой ЕL.
В зоне IV система находится в твердом состоянии. Так как длина горизонтальной площадки, соответствующая кристаллизации эвтектики, пропорциональна количеству эвтектики, то это можно использовать для определения массы эвтектики, которая может быть выделена из смеси любого состава. Для этого необходимо построить треугольник Таммана.
Длины горизонтальных площадок (а, б, в, г, д) откладывают вертикально вниз от СЕМ в точках, отвечающих составам смесей. Соединив нижние концы и точки С и М, получаем треугольник Таммана.
1. Кристаллизация смеси, содержащей 60% кремния, начнется при температуре 1421К.
2. В твердую фазу будет переходить кремний. Расплав будет обогащаться алюминием.
3. При охлаждении системы, содержащей 60% кремния до 1000К, некоторое количество кремния выделится в виде кристаллов. Для определения количества твердой и жидкой фаз применяется правило рычага.
Вес кристаллов кремния так относится к весу жидкой фазы, как отрезок OF относится к отрезку FP. Если вес системы 2 кг, то
mт+ mж = 2 кг,
mж= 2 – mт.
отсюда
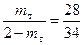 ,
,
решаем уравнение относительно mт:
34 mт + 28 mт = 56,
mт = 0,903 кг.
При Т = 1000К из системы, содержащей 60% кремния, выделится 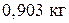 кристаллического кремния.
кристаллического кремния.
4. Кристаллизация этой смеси закончится при температуре 845К – температуре эвтектики.
5. Состав последней капли жидкости соответствует составу эвтектики (10% кремния и 90% алюминия).
6. Массу эвтектики определяем из треугольника Таммана. Треугольник MKD подобен треугольнику MES, следовательно:
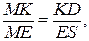
по условию mсистемы = 2 кг => ES = 2, все отрезки замеряем,
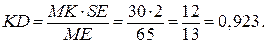
При охлаждении 2 кг смеси, содержащей 60% кремния, выделится 0,923 кг эвтектики.
Читайте также:
lektsia.com
Построение - треугольник - Большая Энциклопедия Нефти и Газа, статья, страница 4
Построение - треугольник
Cтраница 4
Этот вопрос непосредственно связан с вопросом построения треугольника по трем элементам. [46]
Составить подпрограмму для задачи определения возможности построения треугольника из отрезков, длины которых заданы значениями переменных А, В С. [47]
Разность двух векторов находят при помощи построения треугольника, но при этом построении начала данных векторов ( уменьшаемого и вычитаемого) помещаются в одной и той же точке, а вектор, равный по модулю и направлению их разности, должен быть направлен от вычитаемого вектора к уменьшаемому. [48]
Составить подпрограмму для задач определения возможности построения треугольника из отрезков, длины которых заданы значениями переменных А, В, С. [49]
Таким образом, задача сводится к построению треугольника АСМ ( ВСМ) по трем сторонам: а, &, &; построив треугольник АСМ, нетрудно найти точку В - третью вершину искомого треугольника. [50]
Но в школе ограничиваются почти исключительно построением треугольников и притом лишь задачами, разрешимыми при помощи циркуля и линейки. [51]
Необходимо обратить внимание на разницу в построении треугольников сопротивлений ( рис. 5 - 17 и 5 - 23) и треугольников проводимостей ( см. рис. 5 - 27 и 5 - 29), а именно: при построении треугольника сопротивлений активное сопротивление г откладывают по направлению вектора тока /, индуктивное сопротивление XL ( см. рис. 5 - 17) - в перпендикулярном направлении в сторону вращения векторов, а емкостное сопротивление хс ( см. рис. 5 - 23) - в перпендикулярном против вращения векторов. [52]
Величины сил N и Т определяются из построения треугольника сил аналогично предыдущему. [54]
Натуральные величины треугольных граней пирамиды находим методом построения треугольников по трем его сторонам. [55]
Точное положение точки Р может быть зафиксировано построением треугольника Таммана. Коннода ТРР разграничивает области существования жидкого расплава с полиморфными модификациями компонента А. [57]
Однако приведенный результат не является однозначным, поскольку построение треугольника по трем сторонам дает нам второе решение - АаЬс, изображенный на рис. 18, я пунктиром. [58]
Страницы: 1 2 3 4
www.ngpedia.ru
Тамман - Справочник химика 21
Параболический закон роста окисной пленки, установленный впервые Тамманом на примере взаимодействия серебра с парами йода, наблюдали в опытах по окислению на воздухе и в кислороде меди и никеля (при I > 500° С), железа (при I > 700° С) и большого числа других металлов и сплавов при определенных температурах, В табл. 6 приведены параметры диффузии элементов в окислах. [c.59] Для объяснения границ устойчивости Тамман предположил существование сверхструктур (упорядоченного расположения атомов) в твердых растворах, при котором возможно появление защитных плоскостей в решетке сплава, обогащенных или сплошь занятых атомами устойчивого элемента (например, атомами золота в твердом растворе Си + Аи — рис. 227). [c.329]Влияние давления на скорость полимеризации индена и стирола в жидкой фазе изучали Тамман и соавтор (155). Зависимость константы скорости полимеризации от давления выражалась следующими уравнениями [c.147]
Впервые динамический метод был применен Тамманом еще в 1888 г. [c.151]
Тамман установил, что коррозионная стойкость полностью гомогенных твердых растворов в отсутствие заметной диффузии при легировании менее устойчивого металла более устойчивым изменяется не непрерывно, а скачками (рис. 225). Резкое изменение коррозионной стойкости происходит, когда концентрация легирующего элемента достигает атомной доли, или величины, кратной этому числу, т. е. 8, % и т. д. атомной доли — правило п18 Таммана. [c.327]
Адсорбированный кислород насыщает валентности всех (по Тамману, Лангмюру и др.) или наиболее активных (по Стран-скому) поверхностных атомов металла и тем самым снижает его химическую активность. [c.308]
В зависимости от температуры (и давления) наблюдается различный механизм термического превращения диолефинов. При низких температурах и высоких давлениях полимеризация диолефинов имеет цепной характер. Каждая активированная молекула диолефина является началом цепи, в результате которой образуются высокомолекулярные полимеры диолефинов, повидимому открытого строения. Так например, Тамман и соавтор (155) наблюдали, что при температурах 140— 160° С и повышенном давлении изопрен и диметилбутадиен целиком превращались в высокомолекулярные полимеры. [c.124]
Границы устойчивости твердых растворов Си + Аи в различных водных растворах (по Тамману) [c.328]
Возможности препаративного метода сильно ограничены при исследовании таких многокомпонентных систем, как растворы, сплавы, стекла, шлаки. В подобных системах в зависимости от концентраций компонентов и внешних условий наблюдаются изменения физических и химических свойств. Установить природу этих изменений препаративным способом трудно, так как соединения, образующиеся в результате взаимодействия компонентов и обусловливающие новые качественные свойства системы, часто имеют неопределенный состав. Изучение взаимодействия веществ в многокомпонентных системах без выделения образующихся продуктов проводится методом физикохимического анализа. Основы этого метода заложены Д. И. Менделеевым, Ле-Шателье, Г. Тамманом и всесторонне развиты Н. С. Курнаковым (1912—1914). Сущность физико-химического анализа заключается в исследовании функциональной зависимости между численными значениями физических свойств равновесной химической системы [c.166]
Медь, серебро и золото плавятся при температуре около 1000° С, а железо, кобальт и никель — около 1500° С. Поэтому поверхностная и внутренняя температуры рекристаллизации (по Тамману) находятся соответственно в интервалах 150—350° С и 300—600° С, [c.25]
Тамман и соавторы (155) изучали кинетику полимеризации изопрена и диметилбутадиена в жидкой фазе при низких температурах. [c.142]
Наблюдавшиеся Г. Тамманом кривые для зависимости с. з. ц. к. [c.394]
Тамман и соавтор (155) выражают зависимость от давления коп- стант скорости нолимеризации изопрена и диметилбутадиена следую-ш ими уравнениями изопрен (при 160° С) [c.143]
Сплавы золота с медью или серебром сохраняют коррозионную стойкость золота, пока его содержание в сплаве превышает некоторое критическое значение, которое Тамман [1] назвал границей устойчивости. Ниже границы устойчивости сплав корродирует, например в сильных кислотах при этом нераство-ренным остается чистое золото в виде пористого металла или порошка. Такое поведение сплавов благородных металлов известно под названием избирательной коррозии и, очевидно, по характеру сходно с обесцинкованием сплавов медь—цинк (см. разд. 19.2.1). [c.292]
Долгое время принимали, что образование зародышей происходит самопроизвольно (спонтанно). Такую точку зрения развивал Тамман. Он считал, что в некоторых участках пересыщенного раствора, находящегося в метастабильном состоянии, молекулы или ионы растворенного вещества сами по себе без участия каких-нибудь посторонних взвешенных частиц могут располагаться в кристаллическом порядке, образуя мельчайшие зародыши, способные к дальнейшему росту. [c.224]Образование зародышей новой фазы происходит в результате флуктуаций, т. е. самопроизвольного отклонения от равновесного распределения молекул и временного скопления небольшого количества молекул в отдельных участках старой фазы. В тех случаях, когда новая фаза термодинамически более устойчива, чем старая, существует некоторый критический размер зародышей, могущих участвовать в образовании новой фазы. Зародыши меньшего размера, чем критический, имеют тенденцию к исчезновению. Теория процессов, связанных с образованием новых фаз, разработана Гиббсом, Фольмером, Френкелем, Тамманом, Даниловым и др. [c.264]
Исследования воды при высоких давлениях показали, что диаграмма состояния такой системы имеет более сложный вид. Тамман установил, что лед при высоких давлениях может существовать в виде нескольких аллотропных форм. [c.174]
Кристалл зарождается в какой-то физической точке расплава или раствора и затем от этой точки начинается его рост. Вопрос о начальной стадии образования кристаллических зародышей давно привлек внимание ученых. Однако он считается нерешенным и в настоящее время. Большой интерес в учении о кристаллах представляют исследования Г. Таммана, основные выводы из которых обычно излагаются в курсах физической химии, металловедения, металлографии и физики. Г. Тамман исследовал переохлажденные стеклообразные расплавы, главным образом органических веществ, и выдвинул идею о самопроизвольном (спонтанном) зарождении центров кристаллизации в переохлажденных жидкостях. Он полагал, что в некоторых местах переохлажденной жидкости молекулы сами по себе располагаются в кристаллическом порядке и образуют зародыш. [c.229]
М. В. Ломоносов обращал внимание на важность использования различных физических приборов и математических методов для развития химической науки. Инструментальные методы в дальнейшем получили широкое развитие в исследованиях Д. И. Менделеева и Д. П. Коновалова. В конце XIX и начале XX в. Н. С. Курнаков и Г. Тамман создали физико-химический анализ на основании теоретических исследований Вант-Гоффа, Д. В. Гиббса и Ле Шателье. [c.448]
Г. Тамман установил большое влияние на зарождение и рост кристаллов посторонних примесей в растворе или расплаве (частиц кристаллизующегося вещества, частиц других веществ, изоморфных с кристаллизующимися веществами, частиц, которые адсорбируют на своей поверхности молекулы кристаллизующегося вещества). Эти частицы могут служить центрами зарождения кристаллов, уменьшая степень необходимого пересыщения. Исходя из экспериментальных данных Таммана и других исследователей, можно было бы развить приблизительно такие теоретические представления о механизме зарождения кристаллических центров. [c.229]
Однако Тамман в вопросе о зарождении кристаллов исходил из неправильных предпосылок. Он считал, что в каждой жидкости существуют два рода молекул — изотропные и анизотропные и что кристаллы могут образоваться только из анизотропных молекул. Существование таких молекул в опытах не подтверждается. Тамман далее считал, что молекулы одного рода могут переходить в молекулы другого рода, причем скорость перехода мала, но возрастает при повышении температуры. Анизотропные молекулы влияют на изотропные таким образом, что последние превращаются в анизотропные молекулы, которые соответствующим образом размещаются в кристаллической решетке, и вся жидкость может закристаллизоваться. [c.231]
Ранее было отмечено, что ход кристаллизации определяется соотношением скорости зарождения центров и линейной скорости роста кристаллов. На рис. 80 изображено три типа зависимостей числа центров кристаллизации (чц) и скорости кристаллизации (ск) от переохлаждения. Тамман показал, что в зависимости от взаимного расположения кривой скорости кристаллизации и кривой числа центров переохлажденный расплав может или закристаллизоваться, или перейти в стеклообразное состояние. [c.232]
Другая гипотеза возникновения пассивного состояния (Н. Ленг-мюр, Тамман и др.) исходит из положения, что пассивное состояние возникает в результате образования на поверхности металла слоя адсорбированного кислорода при взаимодействии между металлом и раствором, содержащим окислитель. [c.271]
XX вв. Именно исследование явлений брожения выявило две противоположные, но отнюдь не альтернативные концепции в изучении биокатализа вообще. Их только весьма условно можно назвать химической и биологической. Они выступали во взаимодействии, в-борьбе, субъективно отвергая друг друга, но объективно помогая друг другу познать истину. Наиболее видными адептами химической концепции в XIX в. были Ю. Либих, М. Бертло, X. Ф. Шенбейн, Г. Тамман, Э. Фишер, а биологической, если говорить действительно о видных ученых,— пожалуй, лишь Л. Пастер. Только в [c.176]
Наиболее часто методы физико-химического анализа применяются для изучения равновесных систем, образованных двумя веществами. При этом практически наиболее важной является диаграмма состав — температура плавления . Отдел физико-химического анализа, посвященный изучению таких диаграмм, называется термическим анализом, а сами диаграммы носят название диаграмм плавкости. Начало термическому анализу положил в 1868 г. русский металлург Д. К. Чернов. Особенно много способствовали выработке точных методов исследования в этом направлении Г. А. Тамман и академик Н. С. Курнаков. [c.221]
Основы физш >-химического анализа. В конце XIX и начале XX в. формируется новый раздел химии — физико-химический анализ. Основоположниками нового направления были Гиббс, Ван-дер-Ваальс, Розебом, Тамман, Д.И.Менделеев, Д.П.Коновалов, Н.С.Курнаков. Особая заслуга акад. Курнакова состоит в том, что он разработал основы геометрического анализа диаграмм состояния и создал крупнейшую в мире школу физико-химического анализа. Основная задача этого раздела химии состоит в измерении физических свойств системы, находящейся в состоянии равновесия, при последовательном изменении ее состава. Результатом такого исследования является диаграмма состав — свойство, представляющая собой геометрическое отражение процессов, которые протекают в системе. Геометрический анализ диаграмм состав — свойство, сочетая в себе наглядность и универсальность, позволяет определить число образующихся в системе фаз, их природу, области их существования и особенности взаимодействия между ними. Это обусловлено возможностью наблюдения за изменениями в системе в процессе химического взаимодействия, не выделяя образующиеся фазы для исследования. Таким образом, химия получила метод, при помощи которого открываются пути непосредственного изучения химических процессов, что представляет собой качественно новую ступень в познании природы вещества. [c.192]
В конце XIX и начале XX в. формируется новый раздел химии — физико-химический анализ. Основоположниками нового направления были Гиббс, Ван-дер-Ваальс, Розебом , Тамман , Д. И. Менделеев, Д. П. Коновалов, Н. С. Курнаков. Особая заслуга акад. Кур-накова состоит в том, что он разработал основы геометрического анализа диаграмм состояния и создал крупнейшую в мире школу физико-химического анализа. Основная задача этого раздела химии [c.322]
Тамман Густав Генрих Иоганн Аполлон (1861—1938)—немецкий фи-зико-химик. Открыл полиморфные модификации льда, изучал влияние давления на полиморфные превращения. Развил положение о природе стекол как переохлажденных жидкостей. Установил диаграммы состояния ряда металлических систем. Иностранный почетный член АН СССР. [c.322]
Для пластичных твердых тел вблизи точки плавления (в основном для металлов) удается реализовать разработанный Тамманом и Уди-ным метод нулевой ползучести. К тонким полоскам фольги шириной веса (рис. I—21). Образцы тщательно термостатируются при температуре несколько ниже температуры плавления в течение достаточно длительного времени. Затем измеряется изменение длины образцов М. В зависимости от веса грузика Р происходит либо удлинение образцов, либо сокращение их длины под действием сил поверхностного натяжения обычно наблюдается линейная зависимость удлинения от приложенной силы. Точке пересечения прямой А1 Р) с осью абсцисс ( нулевой ползучести ) отвечает равенство нагрузки Р силам поверхностного натяжения по периметру фольги. Точное рассмотрение, учитывающее изменение формы образца при постоянстве его объема (ср. с. 34), показывает, что в условие равновесия должен быть введен коэффициент /г, так что [c.41]
Этот закон, называемый параболическим законом окисления, был открыт Тамманом при изучении взаимодействия плоских пластин серебра и меди с хлором. [c.512]
Из первого названного закона следует, что условия соприкосновения при нагревании меняются. По Г. Тамману, стабильность поликристаллических металлов обусловлена наличием между кристаллами пленок, состоящих нз посторонних примесей. При нагревании эти пленки разрушаются и тотчас происходит перемещение атомов, приводящее к уменьшению степени дисперсности. [c.204]
Тамман и Джессен измеряли скорости абсорбции различных газов водой для определения коэффициентов диффузии, устранив конвекцию путем отвердения жидкости при добавлении к ней агар-агара. Однако такие добавки, превращающие жидкость в студень, могут, согласно Куинну и Блейру сами по себе воздействовать на ди4к )узионный процесс или на реакции, сопровождающие абсорбцию газа. Поэтому лучше не вносить дополнительные неясности, связанные с их использованием. [c.77]
При легировании коррозионно-неустойчивого металла атомами металла устойчивого, в данной агрессивной среде, при условии, что оба компонента дают твердый раствор, и при отсутствии в сплаве заметной диффузии, полученный сплав приобретает химическую стойкость только при определенных соотношениях компонентов в сплаве. Эти определенные соотношения для таких двухкомпонентных твердых растворов вытекают нз так называемого правила границ устойчивости твердых раст1 оров, сформулированного Тамманом и выражающего зависимость между концентрацией твердого раствора и его коррозионной устойчивостью (так называемое правило п/8). [c.125]
Брейтенбах (9), так же как и Тамман и соавтор (155), считают полимеризацию индена реакцией 1-го порядка. [c.145]
Некоторые другие сплавы также имеют критические составы, склонные к пассивации. Что впервые было описано Тамманном [41]. Примерами таких составов, полученных по данным, анало- [c.89]
Это уравнение называют логарифмическим. Соответственно, график, построенный в координатах у — g t + onst) или у — — Ig t (при t > onst) имеет вид прямой линии. Логарифмическое уравнение, впервые полученное Тамманном и Кестером [11], отражает поведение многих металлов (Си, Fe, Zn, Ni, Pb, d, Sn, Mn, Al, Ti, Та) на начальных стадиях окисления. Вначале справедливость этого уравнения ставилась под сомнение. Были сделаны попытки вывести уравнения на основе предположений о существовании специфических свойств оксидов, таких как наличие диффузионных барьеров и градиентов ионной концентрации и других. Эти предположения не получили экспериментального подтверждения. С другой стороны, было показано, что логарифмическое уравнение можно вывести из условия, 4TQ скорость окисления контролируется переходом электронов из металла в пленку продуктов реакции, причем эта пленка имеет пространственный электрический заряд во всем своем объеме [7, 12]. Преобладание заряда, обычно отрицательного, в оксидах вблизи поверхности металла, подобно электрическому двойному слою в электролитах, было установлено экспериментально. Таким образом, любой фактор, изменяющий работу выхода электрона (энергию, необходимую для удаления электрона из металла), например ориентация зерен, изменения кристаллической решетки или магнитные превращения (точка Кюри), изменяет скорость окисления, что и наблюдалось в действительности [13—15. Когда толщина пленки превышает толщину пространственно-заряженного слоя, определяющим фактором обычно становится скорость диффузии или миграции сквозь пленку. При этом начинает выполняться параболический закон, и ориентация зерен или точка Кюри перестают оказывать влияние на скорость окисления. Исходя из этого, можно сказать, что в начальной стадии оксидная пленка на металлах [c.193]
Классическими работами в этой области долгое время считались работы Таммана, который исследовал процессы зародышеобразования для 150 различных органических веществ. Тамман придерживался взглядов о возможности самопроизвольного зародышеоб-разования центров кристаллизации в переохлажденных жидкостях. Большой вклад в теорию зарождения кристаллов внесли работы Фольмера, который получил соотношение для работы образования стабильного кристаллического зародыша внутри переохлажденного расплава. Свободная энергия Р образования сферического ядра радиуса г из расплава может быть выражена уравнением [c.52]
Первые основные положения о механизме реакций в смесях твердых веществ были сформулированы Тамманом (1935), затем Хедваллом (1938) и сыграли большую роль в изучении реакций между твердыми веществами, послужили базой для их дальнейшего исследования. Впоследствии представления о механизме твердофазовых реакций были развиты и конкретизированы в работах Вагнера. [c.211]
Согласно Тамману при температуре выше 100° С и повышенных давлениях Имовокл — Уромб = 0,4 см . Следовательно, при повышении давления изобарный потенциал моноклинной серы будет увеличиваться быстрее, чем у ромбической, и поэтому AGi, будучи при низких давлениях отрицательным, должно с ростом р изменить знак, пройдя через нуль. По данным последней строки табл. 16 (Т = 368,6° К) определяем [c.132]
Так как коэффициент диффузии растет с температурой в экспоненциальной зависимости, при такой большой энергии активации быстрое нарастание коэффициента диффузии происходит в довольно узком интервале температур. Еще в начальном периоде изучения реакций с участием твердых веществ это было обнаружено Тамманом и подтверждено Хедваллом и привело к введению понятия характеристическая температура или температура начала реакции . Позже Тамман высказал мысль, что понятие о характеристических температурах можно обосновать, исходя из принципа соответственных состояний. Температура плавления твердого вещества (по абсолютной шкале) характеризует ту степень подвижности частиц в решетке, дальнейшее увеличение которой ведет уже к разрушению кристалла с переходом его в жидкое состояние. Поэтому все вещества в точке плавления находятся в соответственных состояниях. Для однотипных твердых тел одинаковая степень подвижности и, следовательно, одинаковая величина коэффициентов диффузии достигаются при одинаковых [c.220]
Согласно Тамману и Веймарну, образование дисперсной фазы в коллоидной системе при конденсации связано с двумя различными процессами возникновением зародышей (первичных частиц) и их последующим ростом. Зародыши могут возникать только при определенной степени пересыщения раствора. Их появление зависит от многих причин химических свойств реагирующих веществ, характера ассоциации атомов и молекул, вязкости среды, температуры и др. Зародыши захватывают вещество из раствора и продолжают расти до тех пор, пока не исчезнет пересыщение. Процесс роста связан со скоростью отложения растворенного вещества на зародышах и зависит иногда от скорости диффузии к поверхности частиц. [c.106]
В 1888—1892 гг. Г. Тамман в Дерпте выполнил серию работ, 1) которых использовал кинетические нредставления для анализа ферментативных процессов. Он пришел к следующему общему выводу, что пеоргапизовапные ферменты ускоряют гидролитические реакции так же, как и кислоты, по действие первых отличает- [c.356]
Для пластичных твердых тел вблизи точки плавления (в основном для металлов) удаетбя реализовать разработанный Тамманом и Удиным метод нулевой ползучести. К тонким полоскам фольги шириной (1 подвешиваются грузы разного веса (рис. [c.49]
Известно, что уменьшение степени дисперсности можно вызвать нагреванием. Наиболее изучено это явление для случая рекристаллизации поликристаллических материалов. Законы ее сформулированы еще Г. Тамманом (Таттап, 1929). Остановимся на тех из них, которые представляют интерес для графитации. [c.204]
История химии (1976) -- [ c.356 , c.357 ]Основы физико-химического анализа (1976) -- [ c.9 , c.91 , c.92 , c.102 , c.108 , c.126 , c.128 , c.130 , c.147 , c.149 , c.159 , c.165 , c.169 , c.182 , c.203 , c.277 , c.298 , c.302 , c.304 ]
Избранные работы по органической химии (1958) -- [ c.457 , c.467 ]
Связанный азот (1934) -- [ c.150 ]
Химическая литература и пользование ею Издание 2 (1967) -- [ c.105 ]
Мировоззрение Д.И. Менделеева (1959) -- [ c.263 ]
Физическая химия (1961) -- [ c.125 , c.131 ]
Химическое равновесие и скорость реакций при высоких давлениях Издание 3 (1969) -- [ c.322 , c.325 , c.327 ]
Руководство по электрохимии Издание 2 (1931) -- [ c.178 , c.179 , c.253 , c.274 , c.292 ]
История органического синтеза в России (1958) -- [ c.56 ]
Термодинамика химических реакцый и ёёприменение в неорганической технологии (1935) -- [ c.156 ]
Химия протеолиза Изд.2 (1991) -- [ c.358 ]
chem21.info
Эвтектический треугольник - Справочник химика 21
Так как на кривых охлаждения длина горизонтальной площадки, соответствующей кристаллизации эвтектики, пропорциональна количеству эвтектики, то это можно использовать для определения концентрации компонентов в эвтектической точке. Для этого строится треугольник Таммана. Длины горизонтальных площадок аб, вг, де, жз и ик (рис. 31, а) откладывают вертикально вниз от изотермы эвтектики в точках, отвечающих составам систем (рис. 31, б), и пересечение линий, проведенных через точки м, б, г, е, э, и, л, к, з, дает состав эвтектики. [c.239] Эвтектические прямые двойных систем транслируются в область тройного состава в виде линейчатых поверхностей, скользя своими концами по ребрам призмы. Образуемые ими линейчатые поверхности являются плоскостями, совпадающими с гранями призмы и простирающимися до эвтектического треугольника. Эти линейчатые поверхности отвечают концу выделения двух фаз. Они служат, таким образом, солидусом двойных выделений, отделяя область трехфазных равновесий Ж -Ь Т -Ь Та от двухфазной области Тх- - Т2. На диаграммах простого эвтектического типа эта область вырождена в плоскость. [c.305]Выше ликвидуса располагается однофазная жидкая область тройной системы. Между тремя поверхностями ликвидуса и линейчатыми поверхностями располагаются области двухфазных равновесий ЖН-А, Ж + ВиЖ-ЬС. Объемы между линейчатыми поверхностями и эвтектическим треугольником, проектирующиеся [c.306]
Пограничными кривыми поверхности ликвидуса тройного соединения являются линии двойных эвтектик Е е Е , Е е Е , Е е Е пересекающихся в тройных эвтектических точках Е , Е и Е . Эти точки расположены в плоскостях эвтектических треугольников к к к , гп т т и вторичных тройных систем. Кривые со стрелками, исходящие из тройных эвтектических точек, изображают линии двойных эвтектик, соединяющие тройные эвтектические точки с двойными эвтектическими точками частных двойных систел . В остальном строение физико-химических фигур плавкости вторичных тройных систем аналогично диаграмме [c.343]
При построении зависимости свойств от состава для многофазной системы необходимо учитывать априорную информацию о строении изучаемой системы. Поверхность ликвидуса в системе эвтектического типа представляет собой три пересекающиеся поверхности первичной кристаллизации каждой фазы. Предлагается [38] аналитически описать каждую из этих поверхностей, применяя симплекс-решетчатые планы, затем найти линии их пересечения и точку пересечения этих линий. Поверхности первичной кристаллизации молено выделить при помощи вспомогательного треугольника, вершинами которого служат точки двойных эвтектик двойных диаграмм (рис. 51, в). Образовавшиеся новые треугольники I, П и П1 рассматриваются как исходные. Для рассматриваемой системы РЬ—Сс1—В1 внутри каждого треугольника был реализован неполно кубический симплекс-решетчатый план (табл. 68). [c.268]
Состав а лежит в области кристаллизации анортита и принадлежит фазовому треугольнику анортит — волластонит — ЗЮг. Выделение первичной кристаллической фазы — анортита начинается при 1400° и идет вдоль линии анортит — точка а до пограничной кривой между анортитом и волластонитом. По пограничной кривой путь кристаллизации пойдет вверх к эвтектической точке с температурой плавления 1170° (точка температурного максимума на этой пограничной кривой лежит ниже, в точке пересечения ее с соединительной прямой анортит — волластонит). Кристаллизация расплава а заканчивается в эвтектической точке с выделением анортита, волластонита и тридимита. [c.143]
На листе миллиметровой бумаги построить диаграмму плавкости в координатах температура — состав. Через точки температур конца кристаллизации провести линию солидуса. С помощью треугольника Таммана, построенного под диаграммой плавкости, определить состав эвтектической смеси и перенести его на линию солидуса. Провести через точки температур начала кристаллиза-цпи плавные кривые ликвидуса. Приняв, что изучаемая система идеальная, рассчитать теплоты плавления обоих веществ с помощью уравнения Шредера. [c.244]
Пятый разрез (рис. 76, д) проведен при температуре ниже температуры кристаллизации эвтектики А — В, но выше тройной эвтектической температуры. Этот разрез пересекает пространство вторичного выделения всех трех компонентов (кристаллизации всех трех двойных эвтектик). Поля диаграммы, отвечающие кристаллизации чистых компонентов, значительно сузились, и расширились поля кристаллизации двойных эвтектик. Площадь, отвечающая жидкому состоянию, лежит в середине и имеет вид криволинейного треугольника. [c.209]
Симплекс-решетчатые планы Шеффе наиболее успешно используют для описания закономерностей в однофазных системах, для однофазных участков сложных систем или если изучаемое свойство определяется только одной фазой. Попытки использовать метод симплексных решеток для построения зависимостей свойств от состава целиком во всей многофазной системе часто оказываются неудачными. Точки симплекс-решетчатого плана могут не совпадать с критическими точками диаграммы, и аналитическое описание не улавливает участки скачкообразного изменения свойств. Например, попытки построения зависимости температуры начала кристаллизации целиком для всей системы эвтектического типа РЬ - d - Bi не привели к успеху, хотя были построены полиномы от второй до четвертой степени включительно (рис. 66, а и 6). При построении зависимости свойств от состава для многофазной системы необходимо учитывать априорную информацию о строении изучаемой системы. Поверхность ликвидуса в системе эвтектического типа представляет собой три пересекающиеся поверхности первичной кристаллизации каждой фазы. Предлагается аналитически описать каждую из этих поверхностей, применяя симплекс-решетчатые планы, затем найти линии их пересечения и точку пересечения этих линий. Поверхности первичной кристаллизации можно выделить при помощи вспомогательного треугольника, вершинами которого служат точки двойных эвтектик двойных диаграмм (рис. 66, в). Образовавшиеся новые треугольники I, II и III рассматриваются как исходные. Для рассматриваемой [c.285]
Всле,а,ствие неудобства пользования перспективными изображениями пространственных диаграмм, обычно пользуются проекцией этой диаграммы на плоскость концентрационного треугольника. Так, на рис. 13.12,6 представлена проекция поверхности ликвидуса — эвтектических линий (e E, егЕ, езЕ) и эвтектической точки Е на плоскости концентрационного треугольника. Для более полной характеристики поверхности ликвидуса изотермы, т. е. линии одинаковых температур начала кристаллизации, могут быть спроектированы на концентрационный треугольник. [c.276]
Если фигуративная точка исходного расплава лежит на вертикали, проходящей через кривую вторичной кристаллизации (например, точка О на рис. 1.13,6), то при опускании ее до этой кривой сразу начинается вторичная кристаллизация (в данном случае Л и С), а первичная отсутствует. Если же точка находится на вертикали, проходящей через прямую, соединяющую проекцию точки тройной эвтектики с вершиной треугольника, то после первичной сразу наступает кристаллизация тройной эвтектики, а вторичная отсутствует. Наконец, если фигуративная точка лежит на вертикали, проходящей через тройную эвтектическую точку, то сразу по достижении последней происходит кристаллизация тройной эвтектики. [c.35]
Добавим еще, что линии А Ех В, В Ез С и А Е С, лежащие в гранях треугольной призмы, основанием которой служит треугольник АВС, представляют собой не что иное как диаграммы двойных систем А—В, В—С, А—С, а точки Е/, Ег, Е2 — их эвтектические точки, которые, если их надо отличить от тройной эвтектической точки Е, называют двойными эвтектическими точками. [c.76]
Укажем, прежде всего, на то, что если фигуративная точка нащей системы попадает в треугольник ЗВС (5С —соединительная прямая), то после затвердевания системы она должна представлять собой механическую смесь В, С и 5 . Однако обе нонвариантные точки — Е и Р — находятся в треугольнике Л5С. Соверщенно ясно, что точка Е — эвтектическая, и ей соответствует одновременная кристаллизация А, 8 и С [c.85]
Первый тип этих точек нам известен. Это эвтектические точки. На рис. 48 дано расположение тройной эвтектической точки относительно фигуративных точек твердых фаз , находящейся в треугольнике, верщинами которого являются Vi, V2, Уз- Вид поверхности ликвидус в окрестности тройной эвтектической точки показан на рис. 49 к тройной эвтектической точке спускаются три моновариантные линии, соответствующие равновесию жидкости с двумя фазами, которые могут выделяться из нее при отнятии от системы теплоты. Мы уже знаем, что такой процесс является конгруэнтным. [c.86]
Физико-химическая фигура плавкости тройной системы простого эвтектического типа состоит, таким образом, из следующих элементов (см. рис. 136) поверхностей ликвидуса А е Ее А, В е Ее В и Сотвечающих первичному выделению компонентов А, В и С, эвтектического треугольника а "Ъ "с", отвечающего концу кристаллизации сплавов тройного состава, линейчатых поверхностей а епервичных выделений компонентов А, В и С, линейчатых поверхностей а"с"с" а", с Ь"Ь "с" [c.305]
Кристаллизация сплава состава М, лежащего внутри эвтектического треугольника, вначале протекает по схеме, сходной с двухфазным выделением кристаллов. Однако в этом случае фигуратив- [c.329]
Для эвтектической точки В элементарным фазовым треугольником будет область АтВп—С—В, и составы, попадающие в эту область, должны закончить кристаллизацию в точке Е. [c.79]
Составы, расположенные в поле кристаллизации С вблизи соединительной прямой, но справа от нее, также проходят довольно сложный путь кристаллизации. Например, расплав состава е при кристаллизации выделяет компонент С, затем на пограничной кривой идет одновременная кристаллизация Л и С. В точке О происходит химическая реакция образования АтВп, на которую расходуются кристаллы Л. Путь кристаллизации в точке О не заканчивается (точка принадлежит фазовому треугольнику С—АтВп—В), а продолжается по пограничной кривой СЕ. В эвтектической точке расплав закристаллизуется с выделением С, АтВп и В. [c.81]
Наибольший интерес представляют те составы, которые являются основой промышленных стекол. Эти составы охватывают поля кристаллизации девитрита, волластонита - a0-Si02 и прилегающие к ним области. Они относятся к наиболее легкоплавким в системе. Почти все указанные составы попадают в один и тот же элементарный фазовый треугольник ЫзгО-25102—НагО-ЗСаО-65102— 5Ю2 и заканчивают кристаллизацию в эвтектической точке О (самая низкотемпературная эвтектика в системе — температура плавления 725°, состав в массовых долях 21,3% КагО 5,2% СаО и 73,5% SIO2). [c.124]
Рассмотрим один из сравнительно сложных путей кристаллизации, соответствующий расплаву а, точка состава которого лежит в области кристаллизации лейцита, но относится к фазовому треугольнику SIO2—К2О-АЬОз-6SIO2—КгО-45102- Путь кристаллизации должен закончиться в эвтектической точке с температурой плавления 710°. [c.136]
В поле кордиерита пути кристаллизации идут по прямым, исходящим из точки состава 2 2 5. Заканчивается кристаллизация в эвтектических точках с температурами 1355°, если точка заданного состава лежит в фазовом треугольнике кордиерит — протоэнстатит — тридимит, и 1365° для фазового треугольника кордиерит — протоэнстатит — форстерит. Только незначительная часть составов этой области, принадлежащих фазовому треугольнику кордиерит — форстерит — шпинель, заканчивает кристаллизацию в точке двойного подъема с температурой 1370°. [c.140]
Диаграмма плавкости политерма растворимости) изображается в виде прямой трехгранной призмы, основанием которой служит треугольник состава, а по высоте отложена температура (рис. 124). Точки а, Ь ц с представляют температуры плавления чистых веществ — соответственно А, В и С . На боковых гранях призмы нанесены кривые аЕф, сЕаЬ и сЕ ,а кристаллизации двойных систем. Так как прибавление третьего компонента понижает температуру плавлення смеси двух других, то, например, введение в эвтектическую смесь А + В (точка Е ) вещества С вызовет понижение температуры кристаллизации — получится идущая книзу и внутрь призмы кривая Е Е равновесия тройной раствор — твердые А + В . Аналогично образуются кривые Е2Е и Е Е (их иначе называют пограничными). Все они сходятся в точке Е (тройная эвтектика), в которой раствор насыщен всеми компонентами это — наиболее легкоплавкая смесь. [c.318]
ДЛИНЫ горизонтальных участков на кривых охлаждения. Продолжительность эвтектических остановок пропорциональна весу кристаллизующейся эвтектики. Она равна нулю у чистых компонентов и достигает наибольшего значения у сплава эвтектического состава. Измерив по кривым охлаждения продолжительность эвтектических остановок, откладываем перпендикулярно к оси состава или эвтектической прямой отрезки, длина которых пропорциональна продолжительности кристаллизации эвтектики. Через концы перпендикуляров проводим две прямые aD и bD. Получаем треугольник aDo (треугольник Таммана), высота которого D лежит на ординате эвтектики. Поэтому абсцисса Лд точки С дает искомый состав эвтектики. Простейшие бинарные сплавы указанного типа образуют d — Bi, Sb — Pb, Al — Si, Li l — K l, геленит — анортит (рис. 57), диопсид — форстерит и др. [c.183]
Трехкомпонентные эвтектические системы. При часто встречающейся в практических условиях необходимости выделять оба компонента бинарной смеси в чистом состоянии приходится прибегать к более сложному процессу, названному экстрактивной кристаллизацией . Экстрактивная кристаллизация позволяет выделить из бинарной эвтектической системы оба компонента в виде чистых продуктов в результате изменения фазового состояния твердое — жидкость путем добавки третьего компонента [8, 79 ]. Диаграммы фазового состояния для трехкомпонентных систем удобнее всего изображать в виде равностороннего треугольника, строящегося в условиях постоянного давления. Влияние температуры можно показать введением четвертой координаты, в результате чего плоская диаграмма приобретает форму тетраэдра. Вследствие неудобства объемных диаграмм для практического использования влияние температуры изображают в виде проекции на основание тетраэдра, получая таким образом плоскую диаграмму. На рис. 3 представлена такая диаграмма для системы метаксилол — нараксилол—н-гентан. [c.55]
Границы треугольника изображают фазовое равновесие твердое — жидкость для трех бинарных смесей. Кривые, соединяющие бинарные эвтектические точки с тройной эвтектической точкой EiEi, EiEi, E Et), называют кривыми бинарных эвтектик. Любая точка на одной из бинарных эвтектических кривых соответствует тройному жидкому раствору, находящемуся в равновесии с двумя твердьши и одной паровой фазой. В тройной эвтектической точке существует три твердые фазы, находящиеся в равновесии с жидкой и паровой фазами. [c.55]
Особенность треугольных диаграмм, подобных представленной на рис. 3, та, что все возможные тройные растворы, образующиеся при комнатной температуре в результате добавки н-гептана к ксилолам, состав которых соответствует бинарной эвтектической смеси Ei, лежат на прямой, соединяющей точку El с вершиной треугольника, соответствующей и-гептану. Такая прямая линия, разумеется, изображает смесь ксилолов постоянного состава с переменными количествами н-гентана. Однако при низких температурах на рис. 3 видно, что кривая EiEi для бинарной эвтектической системы лежит ниже упоминавшейся прямой смешения. Другими словами, при добавке м-гентана состав жидкой фазы в эвтектической точке (в пересчете на смесь, не содержащую я-гептана) изменяется в сторону повышения содернмния метаксилола. Такое изменение состава эвтектической смеси ксилолов, вызываемое присутствием третьего компонента, и лежит в основе процесса экстрактивной кристалли- [c.55]
В тройных системах Т. т.- точки нонвариантных четырехфазных равновесий (см. Многокомпонентные системы). В эвтектич. или перитектической Т. т. сходятся три пов-сти первичной кристаллизации разл. фаз и соотв. три линии совместной кристаллизации, отвечающие трехфазным равновесиям. Т. т. указывают состав жидкой фазы, находящейся в равновесии с тремя кристаллич. фазами. Эвтектическая Т. т. расположена внзтри концентрац. треугольника, в вершинах к-рого находятся точки состава соответствующих кристаллич. фаз, перитектическая Т. т.- вне этого треугольника. Перитек-тические Т. т. могут быть двух видов точки двойного подъема, в к-рых одна из трех линий совместной кристаллизации отходит от Т. т., понижаясь, а две другие - повышаясь точки двойного спуска, в к-рых две линии совместной кристаллизации отходят с понижением, а одна - с повьшгением. [c.12]
Следует отметить, что состав эвтектики, неизвестный, естественно, заранее, описанным методом можно определить по величине горизонтальных площадок на кривых охлаждения при эвтектической температуре. Эвтектическому составу 2 на рис. 77) будет соответствовать максимальная по времени остановка температуры, т. е. максимальная длина площадки. Откладывая на диаграмме состояния длины указанных площадок для различных составов в виде перпендикуляров, проведенных к горизонтали эвтектической температуры, можно построить треугольник (сс1е), высота которого (Ее) определит эвтектический состав. [c.283]
Плоскость А "В "С ", параллельная треугольнику состава и лроходящая через тройную эвтектическую точку Е, называется солидусом, или поверхностью солидуса диаграммы, так как ниже ее вся система находится в затвердевшем состоянии. [c.77]
На рис. 41 изображена такая плоская диаграмма состпа. ния, причем все обозначения на этом рисунке соответствуют обозначениям на рис. 40 кроме того, на нем тройная эвтектическая точка соединена прямыми АЕ, ВЕ и СЕ с вершинами-треугольника. [c.78]
Затвердевание расплава I (см. рис. 47) происходит так. Так как точка I лежит в треугольнике Л5С, затвердевщий сплав будет представлять собой механическую смесь веществ Л/ S, С и, следовательно, затвердевание расплава кончится в эвтектической точке Е. При охлаждении жидкого расплава I первым начинает выделяться компонент С, в точке М начинается совместная кристаллизация С и В в точке Р идет пе-рйтектический процесс — растворение В и выделение S и С. А так как в расплаве / был недостаток В, то при перитекти-ческом процессе первой израсходуется фаза В, после чего последует моновариантный процесс выделения фаз 5 и С (погра- [c.93]
chem21.info
- Как организовать жизнь на пенсии

- Как определить что любишь человека

- Амбиции реализовать

- Какое наказание можно придумать парню

- Индивидуальные качества личности формируются под влиянием

- Как сказать ему что он мне нравится

- Треугольник жертва
- Какой размер больше нравится девушкам

- Как стать более женственной и нежной и мягкой девушкой

- Какой признак не свойственен самопознанию

- Что спросить у бывшего парня
