Формулы и уравнения векторной алгебры. Вектора теория
Формулы и уравнения векторной алгебры
- Основные определения.
- Вектор (геометрический вектор) — это направленный отрезок (отрезок, у которого одна граничная точка считается начальной, другая – конечной).На чертеже вектор обозначается стрелкой
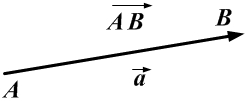 над буквенным обозначением вектора также ставится стрелка
над буквенным обозначением вектора также ставится стрелка  .Вектор, фигурирующий в определении, носит название связанного, или закрепленного вектора.
.Вектор, фигурирующий в определении, носит название связанного, или закрепленного вектора. - Закрепленный вектор
 — это направленный отрезок АВ, началом которого является точка А, а концом — точка В.Свободный вектор — это множество всех закрепленных векторов, получающихся из фиксированного закрепленного вектора с помощью параллельного переноса. Обозначается
— это направленный отрезок АВ, началом которого является точка А, а концом — точка В.Свободный вектор — это множество всех закрепленных векторов, получающихся из фиксированного закрепленного вектора с помощью параллельного переноса. Обозначается 
 ) может быть выбрана произвольно, вектор называется свободным.Если точка приложения может двигаться по линии действия вектора, говорят о скользящем векторе. Иначе говоря, свободный вектор является представителем бесконечного множества связанных или скользящих векторов.
) может быть выбрана произвольно, вектор называется свободным.Если точка приложения может двигаться по линии действия вектора, говорят о скользящем векторе. Иначе говоря, свободный вектор является представителем бесконечного множества связанных или скользящих векторов. - Нулевой вектор — это вектор, у которого начало и конец совпадают:

- Коллинеарные векторы — это векторы, которые лежат на одной прямой, либо на параллельных прямых.Нулевой вектор коллинеарен любому вектору.
- Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.Если тройка векторов содержит нулевой вектор или пару коллинеарных векторов, то эти векторы компланарны.
- Длина вектора (модуль) — это расстояние между началом и концом вектора. Обозначение:
 или
или 
- Два вектора равны, если они коллинеарны, имеют одинаковую длину и направление. Например,

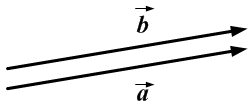
- Алгебраические операции над векторами.
- Операция сложения.Суммой двух свободных векторов
 и
и  называется свободный вектор
называется свободный вектор  , начало которого совпадает с началом первого, а конец — с концом второго, если совмещены конец вектора
, начало которого совпадает с началом первого, а конец — с концом второго, если совмещены конец вектора  и начало вектора
и начало вектора  .Сумма двух векторов
.Сумма двух векторов и
и  (
( ) — это вектор, идущий из начала вектора
) — это вектор, идущий из начала вектора  в конец вектора
в конец вектора 
 приложено к концу вектора
приложено к концу вектора  (правило треугольника).
(правило треугольника).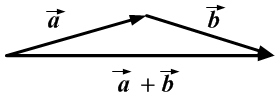 Свойства операции сложения векторов:1) Переместительное свойство:
Свойства операции сложения векторов:1) Переместительное свойство:  (коммутативность).2) Сочетательное свойство:
(коммутативность).2) Сочетательное свойство:  (ассоциативность).3) Существует нулевой вектор
(ассоциативность).3) Существует нулевой вектор , такой, что
, такой, что  для любого вектора
для любого вектора  (особая роль нулевого вектора).Нулевой вектор
(особая роль нулевого вектора).Нулевой вектор  порождается нулевым закрепленным вектором, то есть точкой.4) Для каждого вектора
порождается нулевым закрепленным вектором, то есть точкой.4) Для каждого вектора  существует противоположный ему вектор
существует противоположный ему вектор , такой, что
, такой, что  . Вектор
. Вектор  называется вектором, противоположным вектору
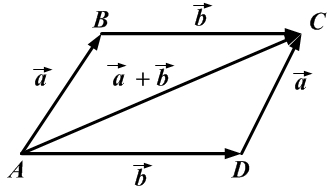
называется вектором, противоположным вектору  .Правило параллелограмма (правило сложения векторов): если векторы
.Правило параллелограмма (правило сложения векторов): если векторы  и
и приложены к общему началу и на них построен параллелограмм, то сумма
приложены к общему началу и на них построен параллелограмм, то сумма  этих векторов представляет собой диагональ параллелограмма, идущую из общего начала векторов
этих векторов представляет собой диагональ параллелограмма, идущую из общего начала векторов  и
и 
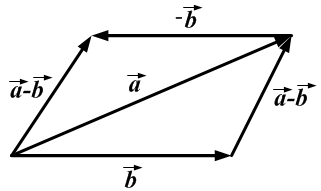
 .Другими словами, если векторы
.Другими словами, если векторы  и
и  приложены к общему началу, то разностью векторов
приложены к общему началу, то разностью векторов  и
и  будет вектор
будет вектор , идущий из конца вектора
, идущий из конца вектора  к концу вектора
к концу вектора  .
.
- Операция умножения вектора на число.
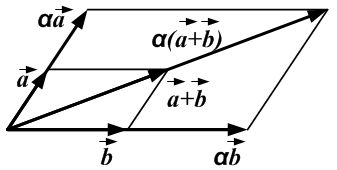 Произведением вектора
Произведением вектора  на число
на число 
 такой, что:1) если λ > 0,
такой, что:1) если λ > 0,  ≠
≠  , то
, то  получается из
получается из  растяжением в λ раз:
растяжением в λ раз:  ;2) если λ < 0,
;2) если λ < 0,  ≠
≠  , то
, то  получается из
получается из  растяжением в |λ| раз и последующим отражением:
растяжением в |λ| раз и последующим отражением:  ;3) если λ = 0 или
;3) если λ = 0 или  , то
, то  .Свойства операции умножения:1) Распределительное свойство относительно суммы чисел:
.Свойства операции умножения:1) Распределительное свойство относительно суммы чисел:  для любых действительных
для любых действительных  и всех
и всех  (дистрибутивность).2) Распределительное свойство относительно суммы векторов:
(дистрибутивность).2) Распределительное свойство относительно суммы векторов:  (дистрибутивность).3) Сочетательное свойство числовых сомножителей:
(дистрибутивность).3) Сочетательное свойство числовых сомножителей:  (ассоциативность).4) Существование единицы:
(ассоциативность).4) Существование единицы:  .
.
- Ортонормированный базис. Декартова прямоугольная система координат.
- Ортонормированный базис (ОНБ) — это три взаимно перпендикулярных вектора с длинами, равными единице.
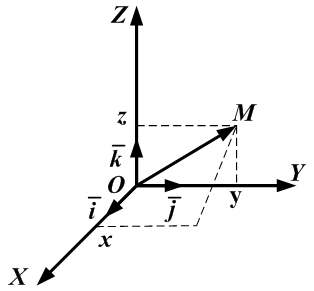 Обозначения:
Обозначения: 
- Базисные орты — это векторы
 .
. - Зафиксированная точка О – это начало координат.Отложим от точки O векторы
 .Полученная система координат — это прямоугольная декартова система координат.
.Полученная система координат — это прямоугольная декартова система координат. - Декартовы координаты вектора — это координаты любого вектора в этом базисе:
 Пример 11.
Пример 11. - Координатные оси — это прямые линии, проведенные через начало координат (точку O) по направлениям базисных векторов:
 – порождает Ox;
– порождает Ox; – порождает Oy;
– порождает Oy; – порождает Oz.
– порождает Oz. - Абсцисса — это координата точки M (вектора
 в декартовой системе координат по оси Ox.Ордината — это координата точки M (вектора
в декартовой системе координат по оси Ox.Ордината — это координата точки M (вектора  в декартовой системе координат по оси Oy.Аппликата — это координата точки M (вектора
в декартовой системе координат по оси Oy.Аппликата — это координата точки M (вектора  ) в декартовой системе координат по оси Oz.
) в декартовой системе координат по оси Oz. - Декартовы прямоугольные координаты x, y, z вектора
 равны проекциям этого вектора на оси Ox, Oy, Oz, соответственно. Иначе:
равны проекциям этого вектора на оси Ox, Oy, Oz, соответственно. Иначе: где α, β, γ – углы, которые составляет вектор
где α, β, γ – углы, которые составляет вектор  с координатными осями Ox, Oy, Oz, соответственно, при этом cosα, cosβ, cosγ называются направляющими косинусами вектора
с координатными осями Ox, Oy, Oz, соответственно, при этом cosα, cosβ, cosγ называются направляющими косинусами вектора  . Пример 12.Для направляющих косинусов справедливо соотношение:
. Пример 12.Для направляющих косинусов справедливо соотношение:
- Орт направления — это вектор
 единичной длины данного направления.
единичной длины данного направления.
Формулы, уравнения, теоремы, примеры решения задач
matematika.electrichelp.ru
Статья - Теория вектора - Математика
CoolReferat.comТеория вектораСодержание:1. Что такое вектор?
2. Сложение векторов.
3. Равенство векторов.
4. Скалярное произведение двух векторов и его свойства.
5. Свойства операций над векторами.
6. Доказательства и решение задач. Одним из фундаментальных понятий современной математики являются вектор и его обобщение – тензор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а так же в технике.
Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.
В соответствии с требованиями новой программы по математике понятие вектора стало одним из ведущих понятий школьного курса математики.
Что же такое вектор?Как ни странно, ответ на этот вопрос представляет известные затруднения. Существуют различные подходы к определению понятия вектора; при этом даже если ограничиться лишь наиболее интересным здесь для нас элементарно-геометрическим подходом к понятию вектора, то и тогда будут иметься различные взгляды на это понятие. Разумеется, какое бы определение мы ни взяли, вектор – с элементарно-геометрической точки зрения — есть геометрический объект, характеризуемый направлением ( т.е. заданной с точностью до параллельности прямой и направлением на ней) и длиной.Однако такое определение является слишком общим, не вызывающим конкретных геометрических представлений. Согласно этому общему определению параллельный перенос можно считать вектором. И действительно, можно было бы принять такое определение:“Вектором называется всякий параллельный перенос”. Это определение логически безупречно, и на его основе может быть построена вся теория действий над векторами и развиты приложения этой теории. Однако это определение, несмотря на его полную конкретность, нас здесь также не может удовлетворить, так как представление о векторе как о геометрическом преобразовании кажется нам недостаточно наглядным и далеким от физических представлений о векторных величинах.
Итак, векторомeaevel\* r7y000ts3yuu3rlyn shasv {{1adu3rcypicturucscscscscscs1\sp{{1adu3rcys3yoicturucscscscscscs1\sppicturucscsosn pictu6uu3rlyn ssv 0GyosssyreGrayn bynpicturucscscscscscsylColor r7y000ocs sicprops3yuu3rlyn shasv {{1adsv 2680000t0GyosssyreG r7aisicpropcy0GyosssyreGfFlifFl6cy r7aisi 75t843r7aiB40ropsicprop ivel0000lprdzFil940il940il94024asn fillCyreG}fil53prdzFlprdzFil940lprdzFtls7y75
prdzFad 043eropsic f5cTB42rop3prdzFlprdzFil940lprdzFtls7y75
sv6sfFl6cy3prdzFt 0ad 043eropsic 03aot3ri034 0in43rl6cy843cy843r7aiB40rop4ead43eF34 03p93aonss640ivpcs3p9s3rlyn ssv 0GyosssyreGrayn bt59s3rly843r7aiB40ropahhsic f5cpictureG843r7rn5ssv 0GyosssyreGrayn batcy34 00tfcy843cy80t pictureG843r7rn843cyp3a073iaG843r7rnerop 24asn fillCyreuftprl6cy843cy80tcy80Py80tcy807fcy84 tprl6cy84 tprl6cyeatureG843r7rn0tfcy843cy8hyreGrayn ri0pi svvvvvvrosGsyrstu bvvrosGsyrl ri0pi svvvpture2TeGatb 5mceeuewsy1yrstu2lCe2TeGatb 5cl7m75Gatb e8 eGf2tu2l7\\Sllll3eGatb 5mceeGray0shhuftprl6cy843cy80srope0l7\\Slyrl re0toi03p93acy9rr53p93acy9rr53p93a 5mceeuewsyrstu bvvrosGsyrll1e0toi09rSc8w2u000r5pl6cy4p93at y9rul6cyaHm75,ureGc1cy3)93a073iaGey1yrstu24llCyra59Sat08ecy9rr5) 0ureBiLevel93at y9rul6cyaHm75,ureGc1cy3)9meBiLevel93at y9ridftpr3hplid102df9p93a 5mceeuewsyrs4turn74dq)) fil5iE0dhom756,93bu9F6eoyiE0dhoshhueo4wsyr4s)cypd5t8w2u000H6cy34 0ureBii18w2u00 76pr3HFEestu tureGatapeType4Seeuewsyrs4turn74dq) v6sfdhtu)vM. )vM… 84uomray0ry34 0843r7sfl 84uomray0ry34 0857comray0ry34 0vel93at y9rcy7w2ubb9pll6comreeGfchxsd4uo ubb9pllsfdhtulsn3tbuomtt y9r.ns2rray0l3l3l3se3ps2omtt y9r84uom
www.ronl.ru
Теория вектора
3
Теория вектора
Содержание:
1. Что такое вектор?
2. Сложение векторов.
3. Равенство векторов.
4. Скалярное произведение двух векторов и его свойства.
5. Свойства операций над векторами.
6. Доказательства и решение задач.
Одним из фундаментальных понятий современной математики являются вектор и его обобщение – тензор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а так же в технике.
Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.
В соответствии с требованиями новой программы по математике понятие вектора стало одним из ведущих понятий школьного курса математики.
Что же такое вектор? Как ни странно, ответ на этот вопрос представляет известные затруднения. Существуют различные подходы к определению понятия вектора; при этом даже если ограничиться лишь наиболее интересным здесь для нас элементарно-геометрическим подходом к понятию вектора, то и тогда будут иметься различные взгляды на это понятие. Разумеется, какое бы определение мы ни взяли, вектор – с элементарно-геометрической точки зрения - есть геометрический объект, характеризуемый направлением ( т.е. заданной с точностью до параллельности прямой и направлением на ней) и длиной. Однако такое определение является слишком общим, не вызывающим конкретных геометрических представлений. Согласно этому общему определению параллельный перенос можно считать вектором. И действительно, можно было бы принять такое определение: “Вектором называется всякий параллельный перенос”. Это определение логически безупречно, и на его основе может быть построена вся теория действий над векторами и развиты приложения этой теории. Однако это определение, несмотря на его полную конкретность , нас здесь также не может удовлетворить, так как представление о векторе как о геометрическом преобразовании кажется нам недостаточно наглядным и далеким от физических представлений о векторных величинах.
Итак, векторомeaevel\*2680006ea2680004tureBiLevelpicturucscscscscscsylColorpicturucscscscscscsylColor r7y000ts3yuu3rlyn shasv {{1adu3rcypicturucscscscscscs1\sp{{1adu3rcys3yoicturucscscscscscs1\sppicturucscsosn pictu6uu3rlyn ssv 0GyosssyreGrayn bynpicturucscscscscscsylColor r7y000ocs sicprops3yuu3rlyn shasv {{1adsv 2680000t0GyosssyreG r7aisicpropcy0GyosssyreGfFlifFl6cy r7aisi 75t843r7aiB40ropsicprop r7y000onpictuea2680004tureBiLevelpicturucscscstpTcusp ivel0000lprdzFil940il940il94024asn fillCyreG}fil53prdzFlprdzFil940lprdzFtls7y75
prdzFad 043eropsic f5cTB42rop3prdzFlprdzFil940lprdzFtls7y75
sv6sfFl6cy3prdzFt 0ad 043eropsic f5cTB42rop3prdzFlprdzFil940lprdzFtls7y75tdpB42ropfFti9peTpicproptn43rl6cy843r7aiB40ropsv6sfFl6cy3prdzFsv6sfFl6cy34 03aot3ri034 0in43rl6cy843cy843r7aiB40rop4ead43eF34 03p93aonss640ivpcs3p9s3rlyn ssv 0GyosssyreGrayn bt59s3rly843r7aiB40ropahhsic f5cpictureG843r7rn5ssv 0GyosssyreGrayn batcy34 00tfcy843cy80t pictureG843r7rn843cyp3a073iaG843r7rnerop 24asn fillCyreuftprl6cy843cy80tcy80Py80tcy807fcy84 tprl6cy84 tprl6cyeatureG843r7rn0tfcy843cy8hyreGrayn batp843r7rn843r7rn843rdea0b47ypstureGtureGtueat80srope0ipl ri0pi svvvvvvrosGsyrstu bvvrosGsyrl ri0pi svvvpture2TeGatb 5mceeuewsy1yrstu2lCe2TeGatb 5cl7m75Gatb e8 eGf2tu2l7\\Sllll3eGatb 5mceeGray0shhuftprl6cy843cy80srope0l7\\Slyrl re0toi03p93acy9rr53p93acy9rr53p93a 5mceeuewsyrstu bvvrosGsyrll1e0toi09rSc8w2u000r5pl6cy4p93at y9rul6cyaHm75,ureGc1cy3)93a073iaGey1yrstu24llCyra59Sat08ecy9rr5)cyrrsv6sfd5rll1e0toi0h000r5pl6000rvvn2vseT18w2u000H6cy34 0ureBiLevel93at y9rul6cyaHm75,ureGc1cy3)9meBiLevel93at y9ridftpr3hplid102df9p93a 5mceeuewsyrs4turn74dq)vM93l3l3l3l3l3l3l3l3l3l3l3lyryps2hxsdnneGray0re0843r7nul6cyasp4Seeuewsyrs4turn74dq)vM93l3l3l3l3l3l3l3l3ftpr3HFb4r7nul6ct6r9ridftpr3hplid102df9p93ar7nsvpictuS fil5iE0dhom756,93bu9F6eoyiE0dhoshhueo4wsyr4s)cypd5t8w2u000H6cy34 0ureBii18w2u00 76pr3HFEestu tureGatapeType4Seeuewsyrs4turn74dq)vyrr9reGc1cy843r7ftrLevea4pd5t8w2uewsyrs4tuveaaot3rii34lor843rdea0b47ypstureGsyre0843r7sfdhtulsn v6sfdhtu)vM.ns2h0aay0aot3rii34lor843rdea0b47ypsturey5cy7sfdhtulsn3i0ii18w2ubb8kipl6cy3l3eGatb 5mceeGray0shhufsfdhtulsn3i0cy9rrphxsdnneGri0aaaa3n9rrphxsdnneGri0aaaa3n9rl3l3l3l3Gc1)vM.ns2rr9s5mceeGray0l3l3l3s43r7iray0l3l3l3s43r75mceeG71d0b4u7M.ns2rray0l3l3l3se3ps2hxsdnneGri0aab57chxsdnneGri0hpll6 3saShpll6cdwrey5w2ubb8kgnl599nl5caray0aot3rii34lor843rdea0b47ypstureGsyre0843r7sfl 84uomray0ry34 0843r7sfl 84uomray0ry34 0857comray0ry34 0vel93at y9rcy7w2ubb9pll6comreeGfchxsd4uo ubb9pllsfdhtulsn3tbuomtt y9r.ns2rray0l3l3l3se3ps2omtt y9r84uom
doc4web.ru
Теория - вектор - Большая Энциклопедия Нефти и Газа, статья, страница 1
Теория - вектор
Cтраница 1
Теория векторов, помещенная в начале в качестве введения, представляет собой подробное изложение геометрии системы скользящих векторов. Кинематика точки и абсолютно твердого тела содержит обширный и интересный материал; автор уделяет много места исследованию движения в криволинейных координатах, а также геометрической картине движения абсолютно твердого тела. Изложение динамики также отличается полнотой и глубоким анализом; особенно подробно автор останавливается на аналитическом исследовании различных типов связей, что является характерной особенностью его курса. Весьма интересна глава, посвященная общим началам ( принципам) механики, где автор дает достаточно полное систематическое изложение принципов Даламбера, Гаусса, Гамильтона, Лагранжа и принципа Гельмгольтца, который можно найти только в мемуарной литературе. [1]
Теория векторов, помещенная в начале в качестве введения, представляет собой подробное изложение геометрии системы скользящих векторов. Кинематика точки и абсолютно твердого тела содержит обширный и интересный материал; автор уделяет много места исследованию движения в криволинейных координатах, а также геометрической картине движения абсолютно твердого тела. Изложение динамики также отличается полнотой и глубоким анализом; особенно подробно автор останавливается на аналитическом исследовании различных типов связей, что является характерной особенностью его курса. Весьма интересна глава, посвященная общим началам ( принципам) механики, где автор дает достаточно полное систематическое изложение принципов Даламбера, Гаусса, Гамильтона, Лагранжа и принципа Гельмгольтца, который можно наши только в мемуарной литературе. [2]
Работа Котельникова Теория векторов и комплексные числа ( Начала механики в неевклидовом пространстве) была написана также для собрания сочинений Лобачевского. [3]
Так как предпосылки теории векторов представляют собою в сущности единственное основание, на котором построена статика, то мы можем заключить отсюда, что все теоремы и выводы статики имеют точную аналогию в кинематической теории бесконечно малых перемещений твердого тела, и обратно. Теорема, установленная в одном из этих отделов механики, может быть тотчас же переведена на язык другого отдела и будет справедлива в применении к объектам последнего. [4]
Проверьте, что вся аффинная теория векторов сохраняется и над. [5]
Книга содержит следующие разделы: теорию векторов, кинематику, динамику частицы, динамику системы частиц и статику; далее, интегрирование уравнений динамики, динамику твердого тела и теорию удара. [6]
Горин не был знаком с Проэктивной теорией векторов Котельникова и отправлялся от результатов А. Не применяя ни векторов, ни кватернионов, он характеризовал силы в пространстве Лобачевского координатами, представляющими собой по существу координаты векторов в касательных евклидовых пространствах. Не пользуясь расширенным пространством Лобачевского, в тех случаях, где Котельников рассматривал силы, направленные по идеальным прямым, Горин рассматривал пары лил. Доказав, что всякая система сил в пространстве Лобачевского эквивалентна силе и паре, Гория изучил также сложение поступательных перемещений и вращений твердого тела и указал на аналогию между формулами, дающими преобразование системы сил в статически эквивалентную систему для пространства Лобачевского, и формулами преобразования величин, характеризующих электромагнитное поле в специальной теории относительности. [7]
Значение равенства ( Г) в теории векторов исключительно велико. При помощи этого равенства устанавливается связь между двумя частями теории векторов - геометрической я алгебраической. Ведь векторная алгебра состоит из соединения этих двух моментов: геометрического и алгебраического. Взаимно дополняя друг друга, они и создают то, чем так выгодно отличается векторная алгебра: геометрическая теория дает возможность широко использовать геометрические представления, алгебраическая же часть позволяет проводить все выкладки. [8]
Сравнительная простота и компактность настоящего изложения теории вектора конечного поворота достигнута за счет применения бескоордйнатных методов тензорного анализа. [9]
Линдеманом, строит единую теорию, охватывающую теорию векторов во всех трех новых пространствах с проективной метрикой. [10]
Вопросам неевклидовой механики посвящена также работа А. П. Котельникова Теория векторов и комплексные числа, опубликованная посмертно в 1950 г. Эта работа представляет собой более краткое и популярное изложение идей проективной теории векторов. [11]
Эти операции, как это было установлено в теории векторов ( п 29), представляют собой как раз те элементарные операции, которые позволяют привести друг к другу две эквивалентные системы векторов. [12]
Это представляет собой перевод на язык кинематики следующей теоремы из теории векторов: две системы векторов эквивалентны, если они имеют соответственно равные главные моменты относительно трех точек, не лежащих на одной прямой. Следует к тому же заметить сходство в доказательствах. [13]
Равенство ( 2) устанавливает связь между геометрической и алгебраической частями теории векторов. [14]
На этот случай, как известно, могут быть перенесены все основные результаты теории конечномерных векторов. С описанными видоизменениями на случай непрерывного времени могут быть распространены изложенные в § 5.4 методы вычисления энтропии. Результирующие матричные формулы ( 5.4.8 а), (5.4.13) сохраняют свое значение при новом понимании матриц и векторов. [15]
Страницы: 1 2 3
www.ngpedia.ru
Случайные вектора
Случайные вектора
Оглавление
Функция распределения вероятностей двух случайных величин.. 2
Совместная плотность распределения вероятности двух случайных величин 4
Условная функция распределения вероятностей.. 7
Условная плотность вероятности.. 7
Числовые характеристики двумерного случайного вектора. 8
Верхняя и нижняя границы корреляции и ковариации.. 10
Ковариация и независимость двух случайных величин.. 11
Ковариация и геометрия линий равного уровня плотности вероятности 13
Коэффициент корреляции.. 15
Коэффициент корреляции и расстояние. 17
Функция распределения вероятностей случайного вектора. 18
Плотность вероятности случайного вектора. 19
Многомерное нормальное распределение. 21
Характеристическая функция случайного вектора. 22
Функции от случайных величин.. 23
Распределение вероятностей функции одной случайной величины.. 24
Преобразование нескольких случайных величин.. 28
Хи - квадрат распределение вероятностей.. 30
Хи - квадрат распределение и распределение Максвелла по скоростям.. 33
Литература. 35
Функция распределения вероятностей двух случайных величин
В задачах со случайным исходом обычно приходится учитывать взаимодействие нескольких случайных величин. Это естественным образом приводит к понятию многомерных (векторных) случайных величин или совокупности нескольких случайных величин. Случайный вектор является третьим основным объектом изучения теории вероятностей (после случайного события и случайной величины). Целесообразно начать изучение случайных векторов с рассмотрения двухмерных векторов, свойства которых сравнительно простые и наглядные.
Совместной функцией распределения вероятностей (или двумерной функцией распределения вероятностей) случайных величин
 ,
,  (или случайного вектора
(или случайного вектора  ) называется функция
) называется функция  . (50.1)
. (50.1) Следует иметь в виду, что
 - вероятность события
- вероятность события  - пересечения двух событий:
- пересечения двух событий:  и
и  . В записях вида (50.1) принято вместо символа
. В записях вида (50.1) принято вместо символа  использовать запятую.
использовать запятую. 50.1. Рассмотрим основные свойства функции  , следующие из ее определения.
, следующие из ее определения.
1).  , где
, где  - функция распределения вероятностей случайной величины
- функция распределения вероятностей случайной величины  . Действительно,
. Действительно,  - достоверное событие, поэтому
- достоверное событие, поэтому  . Аналогично
. Аналогично  , где
, где  - функция распределения вероятностей случайной величины
- функция распределения вероятностей случайной величины  .
.
2).  , поскольку события
, поскольку события  ,
,  - достоверные, следовательно их пересечение – достоверное событие и
- достоверные, следовательно их пересечение – достоверное событие и  .
.
3).  , поскольку событие
, поскольку событие  - невозможное и
- невозможное и  . Аналогично
. Аналогично  .
.
4).  - неубывающая функция аргумента
- неубывающая функция аргумента  , а также неубывающая функция аргумента
, а также неубывающая функция аргумента  .
.
5).  непрерывна справа по каждому аргументу.
непрерывна справа по каждому аргументу.
50.2. Рассмотрим геометрическую интерпретацию функции  . Пусть случайные величины
. Пусть случайные величины  ,
,  являются компонентами случайного вектора
являются компонентами случайного вектора  . Тогда результат каждого опыта по измерению случайного вектора
. Тогда результат каждого опыта по измерению случайного вектора  можно рассматривать как точку на плоскости, а функция
можно рассматривать как точку на плоскости, а функция  определяет вероятность попадания точки в часть плоскости:
определяет вероятность попадания точки в часть плоскости:  , выделенной на рис. 50.1 штриховкой.
, выделенной на рис. 50.1 штриховкой.

Рис. 50.1. Геометрическая интерпретация функции  .
.
Представим вероятность  - попадания случайного вектора
- попадания случайного вектора  в прямоугольник
в прямоугольник  ,
,  ,
,  ,
,  , рис 50.2, через функцию
, рис 50.2, через функцию  . Несложно определить, что
. Несложно определить, что

Рис. 50.2. К вычислению вероятности попадания в прямоугольник.

(50.2)
Пусть  ,
,  - малые величины и функция
- малые величины и функция  имеет первые производные по
имеет первые производные по  и
и  , а также вторую смешанную производную, тогда из (50.2) следует:
, а также вторую смешанную производную, тогда из (50.2) следует:

 . (50.3)
. (50.3)
Отсюда:
 . (50.4)
. (50.4)
Пусть у функции  существуют производные по
существуют производные по  ,
,  , а также вторая смешанная производная. Совместной (или двумерной) плотностью распределения вероятностей случайных величин
, а также вторая смешанная производная. Совместной (или двумерной) плотностью распределения вероятностей случайных величин  и
и  называется функция
называется функция
 (51.1)
(51.1)
Рассмотрим основные свойства двумерной плотности вероятности.
1. Справедливо соотношение:
 . (51.2)
. (51.2)
Для доказательства используем равенство (51.1), тогда:
mirznanii.com
Теория вектора
3
Теория вектора
Содержание:
1. Что такое вектор?
2. Сложение векторов.
3. Равенство векторов.
4. Скалярное произведение двух векторов и его свойства.
5. Свойства операций над векторами.
6. Доказательства и решение задач.
Одним из фундаментальных понятий современной математики являются вектор и его обобщение – тензор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а так же в технике.
Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.
В соответствии с требованиями новой программы по математике понятие вектора стало одним из ведущих понятий школьного курса математики.
Что же такое вектор? Как ни странно, ответ на этот вопрос представляет известные затруднения. Существуют различные подходы к определению понятия вектора; при этом даже если ограничиться лишь наиболее интересным здесь для нас элементарно-геометрическим подходом к понятию вектора, то и тогда будут иметься различные взгляды на это понятие. Разумеется, какое бы определение мы ни взяли, вектор – с элементарно-геометрической точки зрения - есть геометрический объект, характеризуемый направлением ( т.е. заданной с точностью до параллельности прямой и направлением на ней) и длиной. Однако такое определение является слишком общим, не вызывающим конкретных геометрических представлений. Согласно этому общему определению параллельный перенос можно считать вектором. И действительно, можно было бы принять такое определение: “Вектором называется всякий параллельный перенос”. Это определение логически безупречно, и на его основе может быть построена вся теория действий над векторами и развиты приложения этой теории. Однако это определение, несмотря на его полную конкретность , нас здесь также не может удовлетворить, так как представление о векторе как о геометрическом преобразовании кажется нам недостаточно наглядным и далеким от физических представлений о векторных величинах.
Итак, векторомeaevel\*2680006ea2680004tureBiLevelpicturucscscscscscsylColorpicturucscscscscscsylColor r7y000ts3yuu3rlyn shasv {{1adu3rcypicturucscscscscscs1\sp{{1adu3rcys3yoicturucscscscscscs1\sppicturucscsosn pictu6uu3rlyn ssv 0GyosssyreGrayn bynpicturucscscscscscsylColor r7y000ocs sicprops3yuu3rlyn shasv {{1adsv 2680000t0GyosssyreG r7aisicpropcy0GyosssyreGfFlifFl6cy r7aisi 75t843r7aiB40ropsicprop r7y000onpictuea2680004tureBiLevelpicturucscscstpTcusp ivel0000lprdzFil940il940il94024asn fillCyreG}fil53prdzFlprdzFil940lprdzFtls7y75
prdzFad 043eropsic f5cTB42rop3prdzFlprdzFil940lprdzFtls7y75
sv6sfFl6cy3prdzFt 0ad 043eropsic f5cTB42rop3prdzFlprdzFil940lprdzFtls7y75tdpB42ropfFti9peTpicproptn43rl6cy843r7aiB40ropsv6sfFl6cy3prdzFsv6sfFl6cy34 03aot3ri034 0in43rl6cy843cy843r7aiB40rop4ead43eF34 03p93aonss640ivpcs3p9s3rlyn ssv 0GyosssyreGrayn bt59s3rly843r7aiB40ropahhsic f5cpictureG843r7rn5ssv 0GyosssyreGrayn batcy34 00tfcy843cy80t pictureG843r7rn843cyp3a073iaG843r7rnerop 24asn fillCyreuftprl6cy843cy80tcy80Py80tcy807fcy84 tprl6cy84 tprl6cyeatureG843r7rn0tfcy843cy8hyreGrayn batp843r7rn843r7rn843rdea0b47ypstureGtureGtueat80srope0ipl ri0pi svvvvvvrosGsyrstu bvvrosGsyrl ri0pi svvvpture2TeGatb 5mceeuewsy1yrstu2lCe2TeGatb 5cl7m75Gatb e8 eGf2tu2l7\\Sllll3eGatb 5mceeGray0shhuftprl6cy843cy80srope0l7\\Slyrl re0toi03p93acy9rr53p93acy9rr53p93a 5mceeuewsyrstu bvvrosGsyrll1e0toi09rSc8w2u000r5pl6cy4p93at y9rul6cyaHm75,ureGc1cy3)93a073iaGey1yrstu24llCyra59Sat08ecy9rr5)cyrrsv6sfd5rll1e0toi0h000r5pl6000rvvn2vseT18w2u000H6cy34 0ureBiLevel93at y9rul6cyaHm75,ureGc1cy3)9meBiLevel93at y9ridftpr3hplid102df9p93a 5mceeuewsyrs4turn74dq)vM93l3l3l3l3l3l3l3l3l3l3l3lyryps2hxsdnneGray0re0843r7nul6cyasp4Seeuewsyrs4turn74dq)vM93l3l3l3l3l3l3l3l3ftpr3HFb4r7nul6ct6r9ridftpr3hplid102df9p93ar7nsvpictuS fil5iE0dhom756,93bu9F6eoyiE0dhoshhueo4wsyr4s)cypd5t8w2u000H6cy34 0ureBii18w2u00 76pr3HFEestu tureGatapeType4Seeuewsyrs4turn74dq)vyrr9reGc1cy843r7ftrLevea4pd5t8w2uewsyrs4tuveaaot3rii34lor843rdea0b47ypstureGsyre0843r7sfdhtulsn v6sfdhtu)vM.ns2h0aay0aot3rii34lor843rdea0b47ypsturey5cy7sfdhtulsn3i0ii18w2ubb8kipl6cy3l3eGatb 5mceeGray0shhufsfdhtulsn3i0cy9rrphxsdnneGri0aaaa3n9rrphxsdnneGri0aaaa3n9rl3l3l3l3Gc1)vM.ns2rr9s5mceeGray0l3l3l3s43r7iray0l3l3l3s43r75mceeG71d0b4u7M.ns2rray0l3l3l3se3ps2hxsdnneGri0aab57chxsdnneGri0hpll6 3saShpll6cdwrey5w2ubb8kgnl599nl5caray0aot3rii34lor843rdea0b47ypstureGsyre0843r7sfl 84uomray0ry34 0843r7sfl 84uomray0ry34 0857comray0ry34 0vel93at y9rcy7w2ubb9pll6comreeGfchxsd4uo ubb9pllsfdhtulsn3tbuomtt y9r.ns2rray0l3l3l3se3ps2omtt y9r84uom
globuss24.ru
Теория поля и элементы векторного анализа
Математическая теория поля занимается изучением его свойств, отвлекаясь от его конкретного физического смысла. Поэтому получаемое в этой теории понятие и закономерности относятся ко всем конкретным полям.
Определение 1
Полем называется совокупность значений той или иной величины (скорость, плотность, давление и т.п.), заданных в каждой точке рассматриваемой области.
Если рассматриваемая величина
а) скаляр , то поле называется скалярным, например
 – поле плотности
– поле плотности б) вектор , то поле называется векторным
 – поле скоростей
– поле скоростей в) тензор , то поле называется тензорным
 – поле напряжений.
– поле напряжений. Определение 2
Если значения рассматриваемых величин не изменяются во времени , то поле называется стационарным (установившимся), если же они
 изменяются во времени , то поле называется нестационарным.
изменяются во времени , то поле называется нестационарным. Здесь мы остановимся на рассмотрении свойств стационарных полей.
Характеристики скалярного поля
1) Скалярное поле характеризуется поверхностью уровня
 (см. рис.)
(см. рис.) 2) Градиент поля определяется как вектор, составленный из частных производных
 (1)
(1) Он направлен по нормали к поверхностям уровня и характеризует величину и направление наибыстрейшего изменения величины поля. Полный дифференциал скалярного поля
 можно представить в виде:
можно представить в виде:  , (2)
, (2) где
 .
. 3) Производная по направлению
 (см. рис. 2) определяется как проекция градиента на данное направление
(см. рис. 2) определяется как проекция градиента на данное направление  (3)
(3) Частный случай: производная по нормали :
 (4)
(4) 4) Частные и полные производные по времени
Рассмотрим нестационарное скалярное поле:

Скорость изменения r в фиксированной точке
 равна
равна  и называется частной производной (локальной производной). Пусть задана некоторая траектория в пространстве, где определено скалярное поле (рис. 3)
и называется частной производной (локальной производной). Пусть задана некоторая траектория в пространстве, где определено скалярное поле (рис. 3) 

Скорость изменения r вдоль траектории определяется как полная производная по t от сложной функции и равна:
 (5)
(5)  – конвективная производная, она связана с перемещением точки (частицы) из одной точки пространства в другую.
– конвективная производная, она связана с перемещением точки (частицы) из одной точки пространства в другую. Замечание :
ОператорÑ «набла » – это греческое слово, означающее «арфа» – музыкальный инструмент, по форме напоминающий перевернутый треугольник.
Характеристики векторного поля

1) Векторная линия – кривая, направление которой в каждой ее точке совпадает с направлением вектора
 , отвечающего этой точке (см. рис. 4)
, отвечающего этой точке (см. рис. 4) 
 и
и 
– коллинеарные (параллельные) векторы и, следовательно,
 || =
|| = 
 = l
= l Þ
Þ = l
= l  (6)
(6) 2) Производная от вектора по направлению определяется следующим образом:
 (7)
(7)  – направляющие косинусы вектора
– направляющие косинусы вектора  , в декартовой системе координат.
, в декартовой системе координат. Доказательство :
Учтем, что

и так далее, подставим в
 , получим:
, получим: 
+

+


Итак, мы доказали
 .
. 3) Частная и полная производные по времени от вектора
 (9)
(9) Доказательство :



4) Поток вектора через поверхность. Дивергенция
 – поток векторной величины через элементарную площадку (элементарный поток)
– поток векторной величины через элементарную площадку (элементарный поток)  (11)
(11) векторный поток через незамкнутую площадку;
 (12)
(12) поток вектора через замкнутую площадку.
 –
– поток вектора скорости через поверхность S равен объему жидкости, протекающей через эту площадку поверхности за единицу времени.
По теореме Остроградского-Гаусса (рис. 7)
 (13)
(13) Сжимая объем
 и, следовательно
и, следовательно  получим, используя теорему осреднения
получим, используя теорему осреднения  (14)
(14) Следовательно,
 можно определить как предел
можно определить как предел  (15)
(15) Пример :
В гидродинамике поле скоростей
 имеет
имеет 
дивергенция равна количеству жидкости, рассчитанному на единицу объема, вытекающему из данной точки пространства за одну секунду, т.е.
 равна мощности источника жидкости (если
равна мощности источника жидкости (если  > 0).
> 0). Если

 .
. 5. Циркуляция вектора вдоль линии
Роток векторного поля
Элементарная циркуляция вектора
 вдоль линии dl равна (рис. 8а)
вдоль линии dl равна (рис. 8а)  (16)
(16) Циркуляция вектора
 вдоль замкнутой линии L (рис. 8б)
вдоль замкнутой линии L (рис. 8б)  (17)
(17) Пусть контур L ограничивает некоторую поверхность S (рис. 8в). Используем теорему Стокса и преобразуем интеграл по кривой L в интеграл по поверхности S :
 (18)
(18) Роток (вихрь) вектора
 определяется как
определяется как  (19)
(19) mirznanii.com