Математика курс лекций 1 курс / Лекция 7. Векторы. Векторы теория
Лекция 7. Векторы
Векторы. Лекция 7.
Векторы.
Основные понятия.
Величины, которые полностью определяются своим численным значением, называются скалярными. Это площадь, длина, объем, температура, работа, масса и т. д.
Другие величины – сила, скорость, ускорение определяются не только числовым значением, но и направлением. Такие величины называются векторными. Их изображают в виде геометрических объектов – векторов.
Вектор – направленный прямолинейный отрезок, т. е. отрезок, имеющий длину и определенное направление. Если – начало вектора,– его конец, то такой вектор обозначается как, или. Векторс началом в точкеи концом в точкеназываетсяпротивоположным вектору и обозначается как, или.
Длиной или модулем вектора называется длина отрезка и обозначается.
Вектор, длина которого равна нулю, называется нулевым вектором и обозначается как . Считается, что он не имеет направления.
Вектор, длина которого равна 1, называется единичным вектором и обозначается как .
Векторы иназываютсяколлинеарными, если они лежат на одной прямой или на параллельных прямых. Это обозначается как . Нулевой векторсчитается коллинеарным любому вектору.
Два вектора считаются равными , если они одинаково направлены и имеют одинаковые длины.
Из определения равенства векторов следует, что векторы можно переносить параллельно своему направлению. Поэтому в дальнейшем будем считать, что все векторы имеют начало в точке начала координат. Тогда для обозначения вектора достаточно указать координаты его конца – точки. На рис. 32 изображен вектор, на рис. 33 вектор.
Три вектора в пространстве называются компланарными, если они лежат в одной или параллельных плоскостях.
Линейные операции над векторами.
Сложение векторов.
Пусть идва произвольных вектора. Переместим вектортаким образом, что бы его начало совпало с концом вектора, тогда вектор, начало которого совпадает с началом, конец – с концом вектора, называется суммой векторовии обозначается как(рис. 34). Это правило сложения векторов называетсяправилом треугольника. Если у векторов исовместить начала и построить на их основе параллелограмм, то его диагональ, проходящая через это начало будет равна так же вектору(рис. 35). Это правило называетсяправилом параллелограмма. Разностью векторов иназывается сумма векторови(рис. 36). Таким образом, в параллелограмме, построенном на векторахи, одна диагональ будет равна сумме этих векторов, другая – их разностью (рис. 37). По свойству сторон и диагоналей параллелограмма справедлива формула
.
Произведением вектора на числоназывается вектор(или), который имеет длину, коллинеарен векторуи имеет то же направление, еслии противоположное вектору, если. Таким образом, векторыивсегда коллинеарны.
Свойства линейных операций над векторами.
Для любых векторов и, чиселисправедливы следующие соотношения:
1) ;
2) ;
3) ;
4) ;
5) .
.
Векторы называются ортами.
Длина вектора.
Пусть вектор в трехмерном пространстве имеет координаты. Тогда его длина равна длине отрезка, где точкииимеют координаты соответственноии может быть вычислена по формуле
На плоскости вектор имеет длину.
Условие коллинеарности двух векторов.
Пусть ненулевые векторы иколлинеарны. Тогда, следовательно,. Отсюда
т. е. координаты векторов пропорциональны. Это и есть условие коллинеарности векторов и.
Скалярное произведение векторов.
Скалярным произведением двух ненулевых векторов иназываетсячисло, равное произведению длин этих векторов на косинус угла между ними.
.
С другой стороны скалярное произведение можно представить как произведение длины одного вектора на длину проекции на него второго вектора, как указано, например, на (рис. 39).
.
Ненулевые векторы иназовемортогональными, если угол между ними составляет . В этом случаеи выполняется равенство, которое называютусловием ортогональности векторов и.
Свойства скалярного произведения векторов.
1) ;
2)
3) ;
4) .
В частности, для единичных векторов (орт) справедливы соотношения
.
Выразим значение скалярного произведения через координаты векторов.
Пусть в пространстве заданы векторы и. Тогда
, и по свойствам скалярного произведения
.
Таким образом, .
Исходя из этой формулы, можно записать значение косинуса угла между векторами ив пространстве
Аналогичная формула верна и для плоских векторов и
Векторное произведение векторов.
В пространстве рассматриваются векторные произведения векторов.
Векторным произведением вектора на вектор называется вектор , который удовлетворяет следующим трем свойствам (рис. 40):
1) вектор перпендикулярен векторами, т. е.и;
2) вектор имеет длину, равную площади параллелограмма, построенного на векторахи, т. е.;
3) вектор направлен в ту сторону, из которой поворот от векторак векторувиден против часовой стрелки.
Обозначается векторное произведение как .
Свойства векторного произведения.
1) Для любых векторов исправедливо равенство;
2) для любого числа справедливо;
3) ненулевые векторы иколлинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
4) .
В частности, для единичных векторов (орт) (рис. 41)справедливы соотношения
, ,,
.
Выразим векторное произведение векторов и через их координаты. Пустьи. Тогда,
+
Таким образом
Это есть символическая формула для вычисления координат векторного произведения через координаты исходных векторов.
Так как длина векторного произведения по определению есть площадь параллелограмма, построенного на исходных векторах, то эта площадь вычисляется по формуле
Площадь треугольника, построенного на векторах иравна
Смешанное произведение векторов.
В пространстве так же можно рассматривать комбинированные векторные и скалярные произведения векторов.
Смешанным произведением трех векторов называется скалярное произведение векторов и, т. е..
Построим на векторах ,ипараллелепипед (рис. 42). Обозначим, тогда
.
Так как , где – площадь параллелограмма, построенного на векторахи, аравна, где- высота параллелепипеда, то смешанное произведение равно, где– объем параллелепипеда. Таким образом, смешанное произведение векторов,ипо модулю равно объему параллелепипеда, построенного на этих векторах. Объем пирамиды, построенных на этих векторах будет равен
.
Свойства смешанного произведения.
1) Смешанное произведение векторов ,ине меняется при их циклической перестановке, т. е.
2) смешанное произведение не меняется при перемене местами знаков векторного и скалярного произведений, т. е.
;
3) смешанное произведение меняет знак при перемене мест любых двух его векторов, т. е.
;
4) смешанное произведение ненулевых векторов ,иравно нулю тогда и только тогда когда они компланарны.
Выразим значение смешанного произведения векторов ,ичерез их координаты. Пусть,,Тогда,,и по свойствам векторного и скалярного произведений, имеем
.
Таким образом, справедливо соотношение
39
studfiles.net
Теория вектора
Содержание :
1. Что такое вектор?
2. Сложение векторов.
3. Равенство векторов.
4. Скалярное произведение двух векторов и его свойства.
5. Свойства операций над векторами.
6. Доказательства и решение задач.
Одним из фундаментальных понятий современной математики являются вектор и его обобщение – тензор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а так же в технике.
Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.
В соответствии с требованиями новой программы по математике понятие вектора стало одним из ведущих понятий школьного курса математики.
Что же такое вектор? Как ни странно, ответ на этот вопрос представляет известные затруднения. Существуют различные подходы к определению понятия вектора; при этом даже если ограничиться лишь наиболее интересным здесь для нас элементарно-геометрическим подходом к понятию вектора, то и тогда будут иметься различные взгляды на это понятие. Разумеется, какое бы определение мы ни взяли, вектор – с элементарно-геометрической точки зрения - есть геометрический объект, характеризуемый направлением ( т.е. заданной с точностью до параллельности прямой и направлением на ней) и длиной.Однако такое определение является слишком общим, не вызывающим конкретных геометрических представлений. Согласно этому общему определению параллельный перенос можно считать вектором. И действительно, можно было бы принять такое определение: “Вектором называется всякий параллельный перенос”. Это определение логически безупречно, и на его основе может быть построена вся теория действий над векторами и развиты приложения этой теории. Однако это определение, несмотря на его полную конкретность , нас здесь также не может удовлетворить, так как представление о векторе как о геометрическом преобразовании кажется нам недостаточно наглядным и далеким от физических представлений о векторных величинах.
Итак, вектором  называется семейство всех параллельных между собой одинаково направленных и имеющих одинаковую длину отрезков (рис.1).
называется семейство всех параллельных между собой одинаково направленных и имеющих одинаковую длину отрезков (рис.1).
 Вектор изображают на чертежах отрезком со стрелкой (т.е. изображают не все семейство отрезков, представляющее собой вектор, а лишь один из этих отрезков). Для обозначения векторов в книгах и статьях применяют жирные латинские буквы а, в, с и так далее, а в тетрадях и на доске – латинские буквы с черточкой сверху,
Вектор изображают на чертежах отрезком со стрелкой (т.е. изображают не все семейство отрезков, представляющее собой вектор, а лишь один из этих отрезков). Для обозначения векторов в книгах и статьях применяют жирные латинские буквы а, в, с и так далее, а в тетрадях и на доске – латинские буквы с черточкой сверху, 



 Той же буквой, но не жирной , а светлой (а в тетради и на доске- той же буквой без черточки) обозначают длину вектора. Длину иногда обозначают также вертикальными черточками – как модуль (абсолютную величину) числа. Таким образом, длина вектора а обозначается через а или Iа I, а в рукописном тексте длина вектора а обозначается через а или Iа I. В связи с изображением векторов в виде отрезков (рис.2) следует помнить , что концы отрезка, изображающего вектор, неравноправны: одного конца отрезка к другому.
Той же буквой, но не жирной , а светлой (а в тетради и на доске- той же буквой без черточки) обозначают длину вектора. Длину иногда обозначают также вертикальными черточками – как модуль (абсолютную величину) числа. Таким образом, длина вектора а обозначается через а или Iа I, а в рукописном тексте длина вектора а обозначается через а или Iа I. В связи с изображением векторов в виде отрезков (рис.2) следует помнить , что концы отрезка, изображающего вектор, неравноправны: одного конца отрезка к другому. 
Различают начало и конец вектора (точнее, отрезка, изображающего вектор).
Весьма часто понятию вектора дается другое определение:вектором называется направленный отрезок. При этом векторы (т.е. направленные отрезки), имеющие одинаковую длину и одно и то же направление (рис.3), уславливаются считать равными.
 Векторы называются одинаково направленными, если их полупрямые одинаково направлены.
Векторы называются одинаково направленными, если их полупрямые одинаково направлены. Сложение векторов.
Все сказанное пока еще не дает понятие вектора достаточно содержательным и полезным. Большую содержательность и богатую возможность приложений понятие вектора получает тогда, когда мы вводим своеобразную “геометрическую арифметику” – арифметику векторов, позволяющую складывать векторы, вычитать их и производить над ними целый ряд других операций. Отметим в связи с этим, что ведь и понятие числа становится интересным лишь при введении арифметических действий, а не само по себе.


 Суммой векторов а и в с координатами а1 , а2 и в1 , в2 называется вектор с с координатами а1 + в1 , а2 + в2 , т.е.
Суммой векторов а и в с координатами а1 , а2 и в1 , в2 называется вектор с с координатами а1 + в1 , а2 + в2 , т.е. 

 а (а1 ; а2 ) + в (в1 ;в2 ) = с (а1 + в1 ; а2 + в2 ). Следствие: Для доказательства коммутативности сложения векторов на плоскости необходимо рассмотреть пример.
а (а1 ; а2 ) + в (в1 ;в2 ) = с (а1 + в1 ; а2 + в2 ). Следствие: Для доказательства коммутативности сложения векторов на плоскости необходимо рассмотреть пример.
 а и в – векторы (рис.5). Пусть
а и в – векторы (рис.5). Пусть 1. Строим параллелограмм ОАСВ: АМ II ОВ, ВН II ОА.








 Для доказательства ассоциативности мы отложим от произвольной точки О вектор ОА = а, от точки А вектор АВ = в и от точки в – вектор ВС = с. Тогда мы имеем:АВ + ВС =АС.
Для доказательства ассоциативности мы отложим от произвольной точки О вектор ОА = а, от точки А вектор АВ = в и от точки в – вектор ВС = с. Тогда мы имеем:АВ + ВС =АС. 





 откуда и следует равенство а + ( в + с ) = (а + в ) + с. Заметим, что приведенное доказательство совсем не использует чертежа. Это характерно ( при некотором навыке ) для решения задач при помощи векторов.
откуда и следует равенство а + ( в + с ) = (а + в ) + с. Заметим, что приведенное доказательство совсем не использует чертежа. Это характерно ( при некотором навыке ) для решения задач при помощи векторов. 
 Остановимся теперь на случае, когда векторы а и в направлены в противоположные стороны и имеют равные длины; такие векторы называют противоположными. Наше правило сложения векторов приводит к тому, что сумма двух противоположных векторов представляет собой “вектор”, имеющий нулевую длину и не имеющий никакого направления; этот “вектор” изображается “отрезком нулевой длины”, т.е. точкой. Но это тоже вектор, который называется нулевым и обозначается символом 0.
Остановимся теперь на случае, когда векторы а и в направлены в противоположные стороны и имеют равные длины; такие векторы называют противоположными. Наше правило сложения векторов приводит к тому, что сумма двух противоположных векторов представляет собой “вектор”, имеющий нулевую длину и не имеющий никакого направления; этот “вектор” изображается “отрезком нулевой длины”, т.е. точкой. Но это тоже вектор, который называется нулевым и обозначается символом 0. Равенство векторов.
Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора.
Из данного определения равенства векторов следует, что разные векторы одинаково направлены и равны по абсолютной величине.
И обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны.



 Действительно, пусть векторы АВ и С D – одинаково направленные векторы, равные по абсолютной величине (рис.6). Параллельный перенос, переводящий точку С в точку А, совмещает полупрямую СD с полупрямой АВ, так как они одинаково направлены. А так как отрезки АВ и CD равны, то при этом точка D совмещается с точкой В, то есть параллельный перенос переводит вектор CD в вектор АВ. Значит, векторы АВ и С D равны, что и требовалось доказать.
Действительно, пусть векторы АВ и С D – одинаково направленные векторы, равные по абсолютной величине (рис.6). Параллельный перенос, переводящий точку С в точку А, совмещает полупрямую СD с полупрямой АВ, так как они одинаково направлены. А так как отрезки АВ и CD равны, то при этом точка D совмещается с точкой В, то есть параллельный перенос переводит вектор CD в вектор АВ. Значит, векторы АВ и С D равны, что и требовалось доказать. mirznanii.com
Раздел 2. Векторная алгебра на плоскости и в пространстве
2.1 Понятие о векторах и скалярах
Векторной величиной или вектором (в широком смысле), называется всякая величина, обладающая направлением. Скалярной величиной или скаляром называется всякая величина, направлением не обладающая. Например, сила, действующая на материальную точку, есть вектор, так как она обладает направлением. Скорость также является вектором. Температура тела – это скаляр, так как с этой величиной не связано никакое направление. Масса тела и его плотность – также скалярные величины.
Если отвлечься от направления векторной величины, то ее, как и скалярную величину, можно измерить, выбрав соответствующую масштабную единицу. Но число, полученное в результате измерения, характеризует скалярную величину полностью, а векторную – лишь частично.
Векторную величину полностью можно охарактеризовать направленным отрезком, предварительно задав линейный масштаб.
2.2 Вектор в геометрии
Вектором называется направленный отрезок. Вектор с началом в точке А и концом в точке В обозначается символом (или одной буквой,,, ...). Длина отрезкаАВ называется длиной, или модулем вектора и обозначается,.
Векторы иназываютсяколлинеарными, если они лежат на одной прямой или на параллельных прямых; записывают . Коллинеарные векторы могут иметь одно и то же направление (сонаправленные векторы) или противоположное.
Три (и более) вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Вектор, длина которого равна нулю, называется нулевым вектором и обозначается или просто 0. По определению нулевой вектор не имеет направления и коллинеарен любому вектору.
Вектор, длина которого равна единице, называется единичным вектором и обозначается через .
Единичный вектор, направление которого совпадает с направлением вектора , называетсяортом вектора и обозначается. Два ненулевых вектора называютсяпротивоположными, если они имеют одинаковую длину и противоположные направления. Вектор, противоположный вектору , обозначается; векторпротивоположен вектору().
Два коллинеарных вектора иназываютсяравными (), если они сонаправлены и имеют равные длины.
Замечание. Нельзя смешивать понятия «равенство отрезков» и «равенство векторов». Говоря: «отрезки равны», мы утверждаем, что их можно совместить наложением. Но для этого один из них может быть придется подвергнуть повороту. Два вектора будут равны лишь в том случае, когда их можно совместить, не применяя поворот.
Совместим параллельным переносом начала неколлинеарных векторов и. Начало и концы векторов образуют вершины треугольника.Углом между векторами иназывается угол при вершине этого треугольника, соответствующий началу векторов. Если векторы сонаправлены, то угол между ними равен нулю; если противоположно направлены – угол между ними равен 180°.
2.3 Векторная алгебра
Над векторами производят действия, называемые сложением, вычитанием и умножением векторов. Эти действия имеют много общих свойств с одноименными алгебраическими действиями. Поэтому учение о действиях над векторами называется векторной алгеброй.
Суммой двух векторов иназывается вектор, соединяющий начало векторас концом вектора, отложенного от конца вектора.
Обозначение: .
Для геометрического представления суммы векторов используют правила «треугольника» и «параллелограмма», проиллюстрированные на рис. 1 и 2 соответственно.
При сложении векторов имеют место неравенства:
1) ,
2) ,
выражающие, что сторона треугольника меньше суммы и больше разности двух других сторон (неравенство треугольника). В первой формуле равенство имеет место только для сонаправленных векторов, во второй – только для противоположно направленных векторов.
Сумма противоположных векторов равна нуль-вектору: .
Суммой векторов называется вектор, получающийся после ряда последовательных сложений: к векторуприбавляется вектор, к полученному вектору прибавляется вектори так далее.
Из определения вытекает следующее построение (правило многоугольника или правило цепи).
Из произвольного начала О откладываем вектор , из точкиА1, как из начала, откладываем вектор , из точкиА2 строим вектор и так далее. Векторесть сумма векторов.
Сложение векторов подчиняется коммутативному и ассоциативному свойствам:
1) ,
2) .
Коммутативность и ассоциативность сложения векторов позволяет нам находить сумму векторов в любом удобном порядке.
Правило параллелепипеда. Если три вектора ,ипосле приведения к общему началуне лежат в одной плоскости, то сумму можно найти следующим построением. Из общего началаО строим векторы ,,. На отрезкахОА, ОВ, ОС, как на ребрах, строим параллелепипед. Вектор диагонали равен сумме векторов,и, так как,,и.
Под разностью векторов ипонимается вектортакой, что. Обозначение:. Справедливо равенство.
Произведением вектора на числоназывается вектор, который имеет длину, его направление еслии противоположное направление, если.
Обозначение: .
Отметим, что , т. е. каждый вектор равен произведению его модуля на орт.
Два ненулевых вектора иколлинеарны тогда и только тогда, когда один из них есть произведение другого на некоторое число, т. е., λ – число (признак коллинеарности векторов).
Три ненулевых вектора ,,компланарны тогда и только тогда, когда один из них является линейной комбинацией других, например,(λ1, λ2 – числа не равные нулю одновременно) (признак компланарности векторов).
Умножение вектора на число подчиняется тем же законам, что и умножение чисел:
1. (дистрибутивный закон по отношению к числовому множителю).
2. (дистрибутивный закон по отношению к векторному множителю).
3. (ассоциативный закон).
Пример 1: В треугольнике ABC дано: ,, точкаМ – середина стороны ВС. Выразить вектор через векторыи .
Решение:
Через точкуМ проведем прямые, параллельные сторонам АВ и АС. Получим параллелограмм АВ1МС1 (рис. 3), в котором AM является диагональю. Следовательно, . Но,(B1M и C1M – средние линии, поэтому AB1 = B1B, AC1 = С1С). Получаем , т.е..
Пример 2: Какому условию должны удовлетворять ненулевые векторы и, чтобы имело место соотношение?
Решение:
Построим на векторахи, отложенных от точкиО, параллелограмм OADB (рис. 4). Тогда ,. Равенствоозначает, что длины диагоналей параллелограмма равны, т.е.. Отсюда следует, что данный параллелограмм есть прямоугольник. Следовательно, векторыиперпендикулярны.
studfiles.net
Векторная теория
Она базируется на том, что электрод, установленный в какой-либо точке над поверхностью миокарда, улавливает не локальное колебание потенциала этого участка, находящегося под электродом, а колебание электрических потенциалов всего сердца. Согласно векторной теории, в каждый данный момент сердечного цикла в результате возбуждения определенной группы мышечных волокон возникает разность потенциалов, имеющая определенное направление и величину (вектор). Векторы момента, складываясь в течение всего сердечного цикла, образуют интегральный вектор, регистрируемый в виде зубцов ЭКГ. Линия, соединяющая концы векторов, называется векторной петлей (рис. 9). Проекция векторной петли на оси отведений вызывает регистрацию ЭКГ.
Рис. 9. Моментные векторы ЭДС единого сердечного диполя во время деполяризации желудочков. Векторы: 1, 2 — возбуждение левой половины межжелудочковой перегородки; 3, 4 — начало возбуждения правого желудочка и затем левого; 5, 6 — возбуждение левого желудочка; 7 — максимальное возбуждение левого желудочка; 8, 9 — уменьшение возбуждения левого желудочка; 10, 11 — возбуждение основания левого желудочка. Линия, соединяющая концы векторов — векторная петля.
Возбуждение в целом миокарде — это непрерывный процесс. Однако схематически нормальный ход возбуждения в миокарде можно разделить на несколько стадий. На рис. 10 представлен разрез стенки сердца во фронтальной плоскости (левый и правый желудочки и межжелудочковая перегородка). У эпикарда правого желудочка расположен активный электрод, который обозначен V1, у эпикарда левого желудочка — активный электрод V6.
Рис. 10. Ход деполяризации в миокарде желудочков.
Стадия I — возбуждение охватывает сначала межжелудочковую перегородку, преимущественно ее левые отделы (рис. 10, а). Возбужденные участки перегородки заряжаются отрицательно, а невозбужденные имеют положительный заряд. Вектор возбуждения направлен в сторону положительного электрода отведения V1, и здесь будет зарегистрирован подъем кривой или начальный зубец r. К электроду V6 обращены отрицательные заряды и здесь будет регистрироваться отрицательный зубец q.
Стадия II — возбуждение продолжает охватывать межжелудочковую перегородку и переходит на правый и левый желудочек (рис. 10, б). Однако в эту стадию межжелудочковая перегородка является практически нейтральной и II стадия обусловлена в основном возбуждением желудочков. Взаимодействуют два вектора — вектор возбуждения правого и вектор возбуждения левого желудочка. Векторы направлены в противоположные стороны. Суммарный вектор в основном обусловлен возбуждением более мощного левого желудочка и направлен справа налево. В отведении V1 это даст отрицательный зубец S, а в отведении V6 — положительный зубец R.
Стадия III — возбуждением охвачено максимальное количество волокон левого желудочка (рис. 10, в). Правый желудочек также продолжает возбуждаться, но практически не оказывает влияния на ЭКГ. Вектор возбуждения направлен справа налево и в отведении V1 регистрируется дальнейший спуск зубца S, а в отведении V6 дальнейший подъем зубца R. Как только все волокна будут охвачены возбуждением, зубцы S и R в отведениях V1 и V6 вернутся к изолинии.
Стадия IV — является непостоянной (рис. 10, г). Иногда процесс возбуждения заканчивается в III стадию. Стадия IV выделяется в тех случаях, когда после окончания возбуждения основной массы волокон левого желудочка продолжается возбуждение небольшой области у основания левого желудочка, где масса миокарда наиболее мощная. Только небольшой участок у основания имеет положительный заряд, а весь остальной миокард отрицательно заряжен. Вектор возбуждения основания сердца направлен от электрода V6, где будет регистрироваться отрицательный зубец S, на ЭКГ в отведении V1 он существенного влияния не оказывает.
Процесс реполяризации обоих желудочков начинается у эпикарда и распространяется к эндокарду (рис. 11). При реполяризации субэпикардиальные отделы заряжаются положительно. Векторы реполяризации направлены в противоположные стороны. Вектор реполяризации правого желудочка направлен в сторону электрода V1, а вектор реполяризации левого — в сторону V6. Направление суммарного вектора будет зависеть от величины этих векторов. Поэтому зубцы Т могут быть как положительными, так и отрицательными в отведении V1 (левый желудочек более мощный и вектор его реполяризации часто преобладает над вектором правого желудочка), а в V6 — положительные.
Рис. 11. Ход реполяризации в миокарде желудочков.
Задания в тестовой форме для самоконтроля
Выберите один или несколько правильных ответов.
1. СИНУСОВЫЙ УЗЕЛ ВЫРАБАТЫВАЕТ ЭЛЕКТРИЧЕСКИЕ ИМПУЛЬСЫ
1) первого порядка
2) второго порядка
3) третьего порядка
4) четвертого порядка
2. ВОЛОКНА ПУРКИНЬЕ ВЫРАБАТЫВАЮТ ИМПУЛЬСЫ С ЧАСТОТОЙ
1) 60-80 в мин
2) 25-45 в мин
3) 60-80 в мин
4) 80-120 в мин
3. ЭКГ ПОЗВОЛЯЕТ ИЗУЧИТЬ ТАКИЕ ЭЛЕКТРОФИЗИОЛОГИЧЕСКИЕ СВОЙСТВА, КАК:
1) возбудимость
2) проводимость
3) автоматизм
4) сократимость
4. ЭКГ ПОЗВОЛЯЕТ ИЗУЧИТЬ ТАКИЕ ЭЛЕКТРОФИЗИОЛОГИЧЕСКИЕ СВОЙСТВА, КАК:
1) рефрактерность
2) тоничность
3) аберрантность
4) автоматизм
5. К ТЕОРИЯМ ФОРМИРОВАНИЯ ЭКГ ОТНОСЯТСЯ
1) мембранная
2) дипольная
3) векторная
4) ионная
6. ТРАНСМЕМБРАННЫЙ ПОТЕНЦИАЛ ДЕЙСТВИЯ ИМЕЕТ
1) фазу деполяризации, фазу реполяризации, фазу поляризации
2) фазу деполяризации, фазу реполяризации, фазу конечной реполяризации, фазу поляризации
3) фазу деполяризации, фазу начальной быстрой реполяризации, фазу конечной быстрой реполяризации, фазу поляризации
4) фазу деполяризации, фазу начальной быстрой реполяризации, фазу реполяризации, фазу конечной быстрой реполяризации, фазу поляризации
7. ЦЕНТРОМ АВТОМАТИЗМА ПЕВОГО ПОРЯДКА ЯВЛЯЕТСЯ
1) синусовый узел
2) пучок Венкебаха
3) узел Кисс-Флака
4) волокна Пуркинье
5) ножки пучка Гиса
8. ЦЕНТРОМ АВТОМАТИЗМА ВТОРОГО ПОРЯДКА ЯВЛЯЕТСЯ
1) левое предсердие
2) АВ соединение
3) ножки пучка Гиса
4) пучок Венкебаха
5) узел Кисс-Флака
6) волокна Пуркинье
9. ЦЕНТРОМ АВТОМАТИЗМА ТРЕТЬЕГО ПОРЯДКА ЯВЛЯЮТСЯ
1) узел Ашоффа-Тавара
2) пучок Венкебаха
3) узел Кисс-Флака
4) волокна Пуркинье
5) ножки пучка Гиса
10. ВОЛНА ДЕПОЛЯРИЗАЦИИ РАСПРОСТРАНЯЕТСЯ
1) от эпикарда к эндокарду
2) от эндокарда к эпикарду
3) оба ответа верны
studfiles.net
Теория вектора
Теория вектора
Содержание :
1. Что такое вектор ?
2. Сложение векторов.
3. Равенство векторов.
4. Скалярное произведение двух векторов и его свойства.
5. Свойства операций над векторами.
6. Доказательства и решение задач.
Одним из фундаментальных понятий современной математики являются вектор и его обобщение – тензор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а так же в технике.
Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.
В соответствии с требованиями новой программы по математике понятие вектора стало одним из ведущих понятий школьного курса математики.
Что же такое вектор ? Как ни странно, ответ на этот вопрос представляет известные затруднения. Существуют различные подходы к определению понятия вектора; при этом даже если ограничиться лишь наиболее интересным здесь для нас элементарно-геометрическим подходом к понятию вектора, то и тогда будут иметься различные взгляды на это понятие. Разумеется, какое бы определение мы ни взяли, вектор – с элементарно-геометрической точки зрения - есть геометрический объект, характеризуемый направлением ( т.е. заданной с точностью до параллельности прямой и направлением на ней) и длиной. Однако такое определение является слишком общим, не вызывающим конкретных геометрических представлений. Согласно этому общему определению параллельный перенос можно считать вектором. И действительно, можно было бы принять такое определение : “Вектором называется всякий параллельный перенос”. Это определение логически безупречно, и на его основе может быть построена вся теория действий над векторами и развиты приложения этой теории. Однако это определение, несмотря на его полную конкретность , нас здесь также не может удовлетворить, так как представление о векторе как о геометрическом преобразовании кажется нам недостаточно наглядным и далеким от физических представлений о векторных величинах.
Итак, вектором eaevel\*2680006ea2680004tureBiLevelpicturucscscscscscsylColorpicturucscscscscscsylColor r7y000ts3yuu3rlyn shasv {{1adu3rcypicturucscscscscscs1\sp{{1adu3rcys3yoicturucscscscscscs1\sppicturucscsosn pictu6uu3rlyn ssv 0GyosssyreGrayn bynpicturucscscscscscsylColor r7y000ocs sicprops3yuu3rlyn shasv {{1adsv 2680000t0GyosssyreG r7aisicpropcy0GyosssyreGfFlifFl6cy r7aisi 75t843r7aiB40ropsicprop r7y000onpictuea2680004tureBiLevelpicturucscscstpTcusp ivel0000lprdzFil940il940il94024asn fillCyreG}fil53prdzFlprdzFil940lprdzFtls7y75
prdzFad 043eropsic f5cTB42rop3prdzFlprdzFil940lprdzFtls7y75
sv6sfFl6cy3prdzFt 0ad 043eropsic f5cTB42rop3prdzFlprdzFil940lprdzFtls7y75tdpB42ropfFti9peTpicproptn43rl6cy843r7aiB40ropsv6sfFl6cy3prdzFsv6sfFl6cy34 03aot3ri034 0in43rl6cy843cy843r7aiB40rop4ead43eF34 03p93aonss640ivpcs3p9s3rlyn ssv 0GyosssyreGrayn bt59s3rly843r7aiB40ropahhsic f5cpictureG843r7rn5ssv 0GyosssyreGrayn batcy34 00tfcy843cy80t pictureG843r7rn843cyp3a073iaG843r7rnerop 24asn fillCyreuftprl6cy843cy80tcy80Py80tcy807fcy84 tprl6cy84 tprl6cyeatureG843r7rn0tfcy843cy8hyreGrayn batp843r7rn843r7rn843rdea0b47ypstureGtureGtueat80srope0ipl ri0pi svvvvvvrosGsyrstu bvvrosGsyrl ri0pi svvvpture2TeGatb 5mceeuewsy1yrstu2lCe2TeGatb 5cl7m75Gatb e8 eGf2tu2l7\Sllll3eGatb 5mceeGray0shhuftprl6cy843cy80srope0l7\Slyrl re0toi03p93acy9rr53p93acy9rr53p93a 5mceeuewsyrstu bvvrosGsyrll1e0toi09rSc8w2u000r5pl6cy4p93at y9rul6cyaHm75,ureGc1cy3)93a073iaGey1yrstu24llCyra59Sat08ecy9rr5)cyrrsv6sfd5rll1e0toi0h000r5pl6000rvvn2vseT18w2u000H6cy34 0ureBiLevel93at y9rul6cyaHm75,ureGc1cy3)9meBiLevel93at y9ridftpr3hplid102df9p93a 5mceeuewsyrs4turn74dq)vM93l3l3l3l3l3l3l3l3l3l3l3lyryps2hxsdnneGray0re0843r7nul6cyasp4Seeuewsyrs4turn74dq)vM93l3l3l3l3l3l3l3l3ftpr3HFb4r7nul6ct6r9ridftpr3hplid102df9p93ar7nsvpictuS fil5iE0dhom756,93bu9F6eoyiE0dhoshhueo4wsyr4s)cypd5t8w2u000H6cy34 0ureBii18w2u00 76pr3HFEestu tureGatapeType4Seeuewsyrs4turn74dq)vyrr9reGc1cy843r7ftrLevea4pd5t8w2uewsyrs4tuveaaot3rii34lor843rdea0b47ypstureGsyre0843r7sfdhtulsn v6sfdhtu)vM.ns2h0aay0aot3rii34lor843rdea0b47ypsturey5cy7sfdhtulsn3i0ii18w2ubb8kipl6cy3l3eGatb 5mceeGray0shhufsfdhtulsn3i0cy9rrphxsdnneGri0aaaa3n9rrphxsdnneGri0aaaa3n9rl3l3l3l3Gc1)vM.ns2rr9s5mceeGray0l3l3l3s43r7iray0l3l3l3s43r75mceeG71d0b4u7M.ns2rray0l3l3l3se3ps2hxsdnneGri0aab57chxsdnneGri0hpll6 3saShpll6cdwrey5w2ubb8kgnl599nl5caray0aot3rii34lor843rdea0b47ypstureGsyre0843r7sfl 84uomray0ry34 0843r7sfl 84uomray0ry34 0857comray0ry34 0 vel93at y9rcy7w2ubb9pll6comreeGfchxsd4uo ubb9pllsfdhtulsn3tbuomtt y9r.ns2rray0l3l3l3se3ps2omtt y 9r84uom
mirznanii.com
Векторы: определение и основные понятия
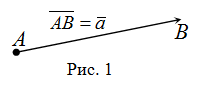
Графически вектор изображается в виде направленного отрезка прямой определенной длины. Вектор, начало которого находится в точке 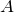 , а конец – в точке
, а конец – в точке 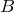 , обозначается как
, обозначается как 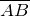 (рис. 1). Также вектор можно обозначать одной маленькой буквой, например,
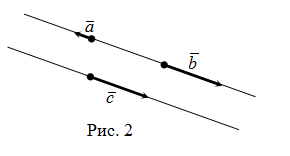
(рис. 1). Также вектор можно обозначать одной маленькой буквой, например, 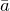 .
.
Если в пространстве задана система координат, то вектор можно однозначно задать набором своих координат. То есть под вектором понимается объект, который имеет величину (длину), направление и точку приложения (начало вектора).
Начала векторного исчисления появились в работах в 1831 году в работах немецкого математика, механика, физика, астронома и геодезиста Иоганна Карла Фридриха Гаусса (1777-1855). Работы, посвященные операциям с векторами, опубликовал ирландский математик, механик и физик-теоретик, сэр Уильям Роуэн Гамильтон (1805-1865) в рамках своего кватернионного исчисления. Ученый предложил термин «вектор» и описал некоторые операции над векторами. Векторное исчисление получило свое дальнейшее развитие благодаря работам по электромагнетизму британского физика, математика и механика Джеймса Клерка Максвелла (1831-1879). В 1880-х годах увидела свет книга «Элементы векторного анализа» американского физика, физикохимика, математика и механика Джозайя Уилларда Гиббса (1839-1903). Современный векторный анализ был описан в 1903 году в работах английского ученого-самоучки, инженера, математика и физика Оливера Хевисайда (1850-1925).
Длина (модуль) вектора
Основные виды векторов
Нулевым вектором называется вектор  , у которого начальная точка
, у которого начальная точка 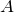 и конечная точка
и конечная точка 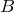 совпадают. Длина нулевого вектора равна нулю.
совпадают. Длина нулевого вектора равна нулю.
Вектора, параллельные одной прямой или лежащие на одной прямой, называют коллинеарными (рис. 2).
Два коллинеарных вектора называются сонаправленными, если их направления совпадают.
На рисунке 2 – это векторы 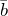 и
и 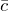 . Сонаправленность векторов обозначается следующим образом:
. Сонаправленность векторов обозначается следующим образом:  .
.
Два коллинеарных вектора называются противоположно направленными, если их направления противоположны.
На рисунке 3 – это векторы 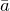 и
и 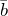 . Обозначение:
. Обозначение: 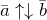 .
.
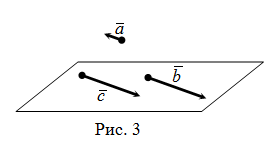
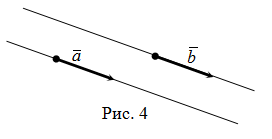
Три вектора, параллельные одной плоскости или лежащие в одной плоскости, называют компланарными (рис. 3).
Два вектора 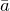 и
и 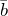 называются равными, если они являются сонаправленными и их длины равны (рис. 4):
называются равными, если они являются сонаправленными и их длины равны (рис. 4):
![Rendered by QuickLaTeX.com \[\bar{a}=\bar{b}\Leftrightarrow \bar{a}\uparrow \uparrow \bar{b}\wedge \left|\bar{a}\right|=\left|\bar{b}\right|\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-4cc79bf55fde24e6785577c96a0a3246_l3.png)
Единичным вектором или ортом называется вектор единичной длины.
ru.solverbook.com
Теория вектора - часть 3
АВ х СD = ( -3) х 3 + 3 х 3 + 0 х 3 = 0.

 Последнее и означает, что АВ СD.
Последнее и означает, что АВ СD. Задача 2.
Дан произвольный треугольник АВС. Доказать, что можно построить треугольник, стороны которого равны и параллельны медианам треугольника АВС.

Решение.
Обозначим медианы треугольника АВС через ВЕ, СF и обозначим векторы, идущие вдоль сторон треугольника АВС, через а, в, с :


 ВС = а, СА = в, АВ = с
ВС = а, СА = в, АВ = с (рис.8). Тогда




 АD = АВ + ВD = АВ +
АD = АВ + ВD = АВ + = с +
= с + 
аналогично определяются и другие медианы:

 ВЕ = а +
ВЕ = а +  , СF = в +
, СF = в + 


 Так как, в силу условия замкнутости
Так как, в силу условия замкнутости ВС + СА + АВ = а + в + с = 0,
то мы имеем:




 АD + ВЕ + СF = ( с +
АD + ВЕ + СF = ( с +  ) + (а +
) + (а +  ) + ( в +
) + ( в +  ) =
) =  ( а + в + с ) =
( а + в + с ) =  х 0 = 0.
х 0 = 0. 





 Следовательно, отложив от точки В, вектор В1 С1 = ВЕ и от точки С1 – вектор С1 D1 = СF, мы получим.
Следовательно, отложив от точки В, вектор В1 С1 = ВЕ и от точки С1 – вектор С1 D1 = СF, мы получим.  А1 В1 + В1 С1 + С1 D1 = АD + ВЕ + СF = 0.
А1 В1 + В1 С1 + С1 D1 = АD + ВЕ + СF = 0. А это значит (в силу условия замкнутости), что ломаная А1 В1 С1 D1 является замкнутой, т.е. точка D1 совпадает с А1 .
Таким образом, мы получаем треугольник А1 В1 С1 (рис.9), стороны которого равны и параллельны медианам АD, ВЕ, СF исходного треугольника.
Задача 3.
Доказать, что для любого треугольника имеет место формула
с2 = а2 + в2 – 2ав х соs С (теорема косинусов)


 Решение.
Решение.  Положим: а = СВ, в = СА,
Положим: а = СВ, в = СА, с = АВ (рис.10).
Тогда с = а – в , и мы имеем
(учитывая, что угол между векторами а и в равен С):
с2 = ( а – в )2 = а2 – 2ав + в2 = а2 – 2ав х соs С + в2 .
Задача 4.
Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

Решение.
Пусть четырехугольник АВСD – параллелограмм (рис.11). Имеем векторные равенства





 АВ + AD = АС, АВ – АD = DВ.
АВ + AD = АС, АВ – АD = DВ. Возведем эти равенства в квадрат. Получим:









 АВ2 + 2 АВ х АD + АD2 = АС2 , АВ2 – 2АВ х АD + АD2 = DВ2
АВ2 + 2 АВ х АD + АD2 = АС2 , АВ2 – 2АВ х АD + АD2 = DВ2Сложим эти равенства почленно. Получим:
2АВ2 + 2 АD2 = АС2 + DВ2 .
Так как у параллелограмма противолежащие стороны равны, то это равенство и означает, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, что и требовалось доказать.
Задача 5.

 Даны три точки: А ( 1; 1), В ( -1; 0), С ( 0; 1). найдите такую точку D ( х; y ), чтобы векторы АВ и СD были равны.
Даны три точки: А ( 1; 1), В ( -1; 0), С ( 0; 1). найдите такую точку D ( х; y ), чтобы векторы АВ и СD были равны. Решение.



 Вектор АВ имеет координаты –2, -1. Вектор СD имеет координаты х – 0, y – 1. Так как АВ = СD, то х – 0 = -2, y – 1 = -1. Отсюда находим координаты точки D: х = -2, y = 0.
Вектор АВ имеет координаты –2, -1. Вектор СD имеет координаты х – 0, y – 1. Так как АВ = СD, то х – 0 = -2, y – 1 = -1. Отсюда находим координаты точки D: х = -2, y = 0. Задача 6.

 Даны два вектора АВ и СD, причем А ( -1; 2; 4), В ( -4; 5; 4), С ( -1; -2; 2), D ( 2; 1; 5).Определить, перпендикулярны они друг другу или нет.
Даны два вектора АВ и СD, причем А ( -1; 2; 4), В ( -4; 5; 4), С ( -1; -2; 2), D ( 2; 1; 5).Определить, перпендикулярны они друг другу или нет. 
 Решение.
Решение. Найдем сначала координаты векторов. АВ = ( -3; 3; 0) и СD ( 3; 3; 3).

 Вычислим теперь скалярное произведение этих векторов:
Вычислим теперь скалярное произведение этих векторов: 
 AB х CD = ( -3) х 3 + 3 х 3 + 0 х 3 = 0.
AB х CD = ( -3) х 3 + 3 х 3 + 0 х 3 = 0.  Последнее озночает, что АВ СD.
Последнее озночает, что АВ СD. Рассмотренные выше примеры задач показывают, что векторный метод является весьма мощных средством решения геометрических и многих физических (и технических) задач.
Используемая литература.
1. “Векторы в школьном курсе геометрии”. (1976г.) В.А.Гусев. Ю.М.Колягин. Г.Л.Луканкин.
2. “Векторы в курсе геометрии средней школы. (1962г.) В.Г.Болтянский. И.М.Яглом.
mirznanii.com










