Волновая функция. Пси квадрат

определяем свои сильные стороны по дате рождения — Пси-Фактор

С точки зрения геометрии словосочетание «Квадрат Пифагора» не имеет никакого значения. Однако в нумерологии существует такой мощный инструмент для эффективной оценки своих возможностей.

Если вы узнаете, чем Вселенная вас наградила при рождении, то вполне вероятно, что ваша жизнь изменится к лучшему в ближайшее время. Очень часто бывает так, что человек просто не догадывается, насколько он силен и в какой именно сфере. Квадрат Пифагора поможет узнать ваши сильные стороны и скорректировать свой жизненный путь, ведь никогда не поздно начать движение по верной дороге. Уверенность в себе поможет вам изменить свою судьбу так, как вы хотите.

Что такое Квадрат Пифагора

Многие слышали из математики про треугольник Пифагора. Этот Квадрат не имеет никакого отношения к геометрии. Он представляет собой девять слов, которые определяют вашу жизнь в той или иной степени. В большинстве случаев используют следующий вариант нумерологического Квадрата:

Всего есть девять пунктов, записанных в трех столбцах и трех строках. Нумерологические расчеты помогут узнать и оценить, какая из сфер для вас наиболее важна. Вам понадобится лишь ваша дата рождения.

Допустим, вы родились 5 февраля 1982 года. Рассчитать необходимо будет 9 чисел для 9 пунктов. Запишем дату вашего рождения как 05021982. После этого можно приступать к расчетам.

Первая строка: «любовь-работа-хобби»

«Любовь» означает умение строить не только любовные, но и дружеские отношения. Это число покажет вам, насколько вы коммуникабельны и способны на эффективное взаимодействие с людьми в целом. Чтобы рассчитать любовь, вам нужно сложить первое и последнее число вашей даты рождения, то есть 0+2. Получаем двойку. Записываем ее рядом с любовью, чтобы не забыть. Минимальное число — 0, а максимально возможное — 11.

Далее считаем «работу». Данный пункт показывает, насколько вы целеустремленная личность. Люди с высокой «работой» чаще добиваются успеха в бизнесе, быстрее понимаются по карьерной лестнице. Если у вас высокий показатель, но вы не можете назвать себя успешными, то вы пока не обрели себя. Если вы родились до 2000 года, то ваше число работы — это сумма цифр месяца рождения. 0502198: 0+2=2. Если вы рождены в ноябре, октябре или декабре, то сложите цифры. 12 месяц — 1+2=3. Если вы были рождены после 2000 года, умножьте полученную цифру на 2 и снова сложите цифры, если получилось число больше, чем 9. Это и будет ваше число работы. Например, вы рождены в декабре после 2000 года. 1+2=3. 3 умножить на 2 — 6. Шестерка — ваше число.

Пункт «хобби» поможет узнать вам, насколько вы уникальны или поверхностны в своих увлечениях. На финансовую сторону жизни это никак не влияет. Если у вас будет высокий показатель, то можете считать себя потенциальным «творцом», способным на создание шедевра. Останется только узнать, в какой сфере вы можете преуспеть — в рисовании, музыке, поэзии и так далее. Маленький результат — это свидетельство того, что вы можете преуспеть в точных науках, так что никто не будет победителем или проигравшим. Чтобы определить свою сильную сторону, вам потребуется взглянуть на дату рождения и найти одинаковые цифры. Тут возможно несколько вариантов:

Если все цифры разные и не повторяются, то вы — абсолютный «технарь», математик или физик. Точные науки — ваше всё.
Если одинаковая цифра встречается два раза, то у вас есть легкие склонности к искусству.
Если цифра встречается три или более раз, то вы с большой вероятностью сможете создать нечто прекрасное. Ваши хобби должны быть высокодуховными. С математикой, скорее всего, у вас проблемы.

Бывают случаи, когда не одна, а две цифры повторяются по два, а то и три раза. Этот расклад тоже весьма символичен, ибо такие люди могут быть сильны почти во всем. Хороший пример — дата рождения 12.12.1988 или 11.02.2001. Подобные сочетания говорят о том, что вы можете стать выдающимися деятелями искусства или учеными.

Вторая строчка: «интеллект-память-труд»

«Интеллект» показывает, насколько хорошо вы можете пользоваться возможностями вашего мозга. Если показатель низкий, то вам трудно дается понимание сложных вещей. Чтобы посчитать «интеллект», нужно взять самое маленькое число и умножить его на самое большое. Ноль брать нельзя. В нашем примере 050282 берем 2 и 8. Заметьте, что год теперь берется в виде последних двух цифр, потому что 1 и 9 априори всегда будут самым маленьким и большим числом. Перемножаем 2 и 8, получаем 16. Диапазон чисел тут большой — от 1 до 81.

«Память». Тут все понятно — чем выше результат, тем лучше ваша память. Нам потребуется только первые четыре цифры вашей даты рождения — день и месяц. Сложите их: 0+2+0+5=7. 7 — довольно мало, но лишь на первый взгляд. Диапазон чисел — от 1 до 9. Если у вас получилось 10, то ваше число — единица. Если больше десяти, то нужно сложить цифры еще раз. 15 — это 1+5=6. Если у вас единица, то вы часто забываете нечто важное, и вам нужно больше времени для того, чтобы запомнить что-то. Естественно, память можно улучшить, но потребуется больше работы над собой для ее улучшения, чем тем, у кого число памяти равно, например, 9.

«Труд» можно заменить на «физические способности». Данный пункт говорит о вашей выносливости и позволяет оценить, является ли это вашей сильной стороной. Отчасти по этому числу можно приблизительно оценить и здоровье. Чтобы получить данное число, вам просто нужно взять число «интеллекта» и записать его наоборот. Если оно было однозначным — например, 1, 2, 3, 4 и так далее, то оно таковым и остается. У выдающих спортсменов это число либо очень низкое, либо очень высокое. Диапазон чисел — от 1 до 97. Очень высокие показатели — это числа меньше 15 и больше 70.

Третья строчка: «удача-мудрость-интуиция»

Эту строку можно считать самой важной. Удача, например, всегда должна быть рядом с вами, но понять ее действие поможет только правильный нумерологический анализ.

Для расчета «удачи» вам потребуется перемножить все числа, кроме нулей, в вашей дате рождения. Берем наш пример — 05021982: 5*2*1*9*8*2= 1440. Складываем цифры и получаем 1+4+4=9. Девятка — высшее число, следовательно этот человек обладает большой удачей. Если у вас маленькое число, то не падайте духом, ибо таким людям удача помогает редко, но метко. В основном это происходит в трудных ситуациях. Лучшее число — 5, потому что для таких людей удача сбалансирована, то есть они могут иметь пути к отступлению и легкие дороги к успеху.

«Мудрость» — это показатель того, насколько хорошо вы способны учиться на своих ошибках. Если в вашей дате рождения встречается хотя бы одна единица или тройка, то мудрость — ваша сильная сторона. Если таких цифр нет, то не расстраивайтесь, ведь мудрость бывает не только врожденной.

«Интуиция». Шестое чувство — это верный помощник в трудных ситуациях. Ученые называют интуицию симбиозом мудрости, удачи, интеллекта. Оценить ее можно лишь приблизительно. Если у вас все в порядке с показателями «мудрости», «удачи» и «интеллекта», то и шестому чувству можно доверять чаще. «Удачу» можно использовать для того, чтобы узнать, когда интуиция будет у вас наиболее острой. Если «удача» меньше 5, то интуиция ваша сильна в критических ситуациях. Если больше 5, то обращайтесь за помощью к шестому чувству, когда вы на гребне волны.

Таким образом, мы заполнили все поля Квадрата Пифагора. Неважно, насколько вы хороши в чем-то, потому что любой результат можно считать положительным. Несмотря на это, вы можете оценить свои способности и правильность выбранного вами пути.

Квадрат Пифагора подскажет вам, как изменить судьбу. Он укажет верный путь, а не откроет формулу счастливой жизни сразу и целиком. Каждый сам меняет свою жизнь и отношение к ней, так что начать нужно с самих себя. Пусть удача будет всегда с вами.

Источник — dailyhoro.ru

psifactor.info

Волновая функция

Волнова́я фу́нкция (функция состояния, пси-функция, амплитуда вероятности) — комплексная функция, используемая в квантовой механике для вероятностного описания состояния квантовомеханической системы. В широком смысле — то же самое, что и вектор состояния.

Вариант названия «амплитуда вероятности» связан со статистической интерпретацией волновой функции: вероятность нахождения частицы (или физической системы) в данном состоянии равна квадрату абсолютного значения амплитуды вероятности этого состояния.

Физический смысл квадрата модуля волновой функции

Волновая функция

\! \Psi(x_1, x_2, \ldots , x_n)

зависит от координат (или обобщённых координат) системы и формируется таким образом, чтобы квадрат её модуля

\! \left|\Psi(x_1, x_2, \ldots , x_n)\right|^2

представлял собой плотность вероятности (для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами

\! x_1=x_{01}, x_2=x_{02}, \ldots , x_n=x_{0n}.

Набор координат, которые выступают в роли аргументов функции, представляет собой полный набор физических величин, которые можно измерить в системе. В квантовой механике возможно выбрать несколько полных наборов величин, поэтому волновая функция одного и того же состояния может быть записана от разных аргументов. Выбранный для записи волновой функции полный набор определяет представление волновой функции. Так, возможны координатное представление, импульсное представление, в квантовой теории поля используется вторичное квантование и представление чисел заполнения или представление Фока и др.

Если волновая функция, например, электрона в атоме, задана в координатном представлении, то квадрат модуля волновой функции представляет собой плостность вероятности обнаружить электрон в той или иной точке пространства. Если эта же волновая функция задана в импульсном представлении, то квадрат её модуля представляет собой плотность вероятности обнаружить тот или иной импульс.

Для волновых функций справедлив принцип суперпозиции, заключающийся в том, что если система может пребывать в состояниях, описываемых волновыми функциями

\! \Psi_1 и \! \Psi_2,

то она может пребывать и в состоянии, описываемом волновой функцией

\! \Psi_\Sigma = c_1 \Psi_1 + c_2 \Psi_2

при любых комплексных

\! c_1 и \! c_2.

Свойства волновой функции

Отметим свойства волновой функции \! \Psi в частном случае трёхмерного пространства в декартовых координатах. В этом случае \! \Psi зависит от трёх переменных \! x, y, z и имеет следующие свойства :

1. Импульс частицы в каждом из направлений \! x, y, z пропорционален первой производной волновой функции, делённой на саму волновую функцию, а именно {p}_x = -i \hbar {\partial \Psi \over\partial x} / \Psi ; \! {p}_y = -i \hbar {\partial \Psi \over\partial y} / \Psi ; {p}_z = -i \hbar {\partial \Psi \over\partial z} / \Psi , где \! {p}_x , \, {p}_y , \, {p}_z — импульсы, i = \sqrt -1 , \hbar = {h \over 2 \pi}. 2. Кинетическая энергия частицы ( {p}_x^2 + {p}_y^2 + {p}_z^2 ) / 2 m пропорциональна второй производной, или кривизне волновой функции, деленной на саму волновую функцию {E}_K = - {{\hbar}^2 \over 2 m } \left( {{\partial}^2 \Psi \over\partial x^2} + {{\partial}^2 \Psi \over\partial y^2} + {{\partial}^2 \Psi \over\partial z^2} \right) / \Psi . 3. Абсолютная величина квадрата функции \left| {\Psi}^2 \right| (то есть сумма возведённых отдельно в квадрат мнимой и действительной частей функции \! \Psi) равна вероятности нахождения частицы в точке с координатами \! ( x, y, z ). Это свойство противоречит законам классической механики, в которой положение частиц в данный момент времени фиксировано. Одно из мнимых ограничений квантовой механики состоит в том, что она с достоверностью определяет лишь время (или, точнее говоря, вероятность) нахождения частицы в данном положении \! ( x, y, z ). В квазиклассическом пределе \hbar \to 0 волновые функции локализуются в дельта-функции, а центры их сосредоточения движутся по классическим траекториям согласно уравнениям Ньютона.

Матричная и векторная формулировки

Любая функция может быть представлена, как бесконечная таблица из её значений, соответствующих каждому аргументу. Если представить в таком виде волновую функцию, то она станет столбцом координат бесконечномерного вектора в Гильбертовом пространстве, то есть, матрицей.

Одна и та же волновая функция в различных представлениях — будет соответствовать выражению одного и того же вектора в разных системах координат. Остальные операции с волновыми функциями так же будут иметь аналоги на языке векторов.

Функциональная (волновая), матричная и векторная формулировки математически эквивалентны.

Философский смысл волновой функции

Волновая функция представляет собой наиболее полное возможное описание квантовомеханической системы. Если в классической механике полное описание системы заключалось в задании местоположений и скоростей всех её частиц и это описание позволяло описать всё будущее и прошлое системы, то в квантовой механике некоторые параметры описать принципиально невозможно. Согласно квантовой механике, описание системы заканчивается на уровне волновой функции и только на уровне волновой функции возможно описать будущее и прошлое системы. Более подробное описание системы, например, с точностью до указания местоположений и скоростей всех её частиц — невозможно и значения этих параметров оказываются более или менее случайными.

Таким образом, создав квантовую механику, наука дошла до состояния, когда она смогла положить конец многовековому противопоставлению детерминизма и индетерминизма. Современная наука утверждает, в мире сочетаются детерминизм и индетерминизм, и границей между ними служит волновая функция.

См. также

mediaknowledge.ru

Смысл пси-функции. Стандартные условия.

Пси-функция не имеет прямого физического смысла, так как является комплексной величиной. Смысл пси-функции сформулировал Макс Борн: квадрат модуля волновой функции даёт плотность вероятности нахождения частицы в некоторой точке с координатами (x,y,z): 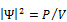; где P – вероятность, V – объём.

Волновая функция должна соответствовать условиям: непрерывности, однозначности, конечности, её производные должны быть непрерывны, она должна быть интегрируема.

12. Принцип суперпозиции. См вопрос 10.

Постулаты квантовой механики.

1. Состояние движения частицы описывается пси-функцией, она удовлетворяет УШ (уравнению Шрёдингера) и стационарным условиям. В соответствии с принципом суперпозиции множество пси-функций, описывающих некоторую механическую систему, образует комплексное линейно-векторное пространство. Каждый вектор этого пространства описывает некоторое состояние системы. Любая суперпозиция векторов этого пространства описывает также состояние системы. Для векторов пространства состояний можно вести скалярное произведение: .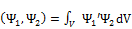

2. Каждой динамической переменной в квантовой теории сопоставляется определенный линейный самосопряжённый оператор: 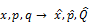. Задача на собственные значения и собственные функции ( 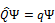) приводит к вещественным собственным значениям ( 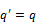). Собственные функции отвечающие различным собственным значениям ортогональны ( 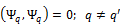). Совокупность собственных функций образует полную систему, где любая пси-функция может быть представлена как линейная .

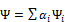3. При измерении числового значения некоторой динамической переменной q, с определенной вероятностью получается одно из собственных значений оператора 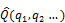. Вероятность получения в опыте значения 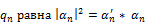, где 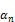- коэффициент разложения пси-функции по собственным значениям оператора 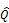. Если пси-функция совпадает с одной из собственных функция, то с вероятностью 1 мы получим при изменении значение .

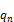Операторы физических величин.

Операторы физической величины определяется исходя из соответствия их выражения в классической механике, принципа соответствия, соотношения неопределенности Гейзенберга и прежде всего в соответствии с требованием совпадения результатов в рамках квантовой формы экспериментальных данных.

1. Оператор координаты: в соответствии с интерпретации пси-функции 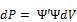, вероятность того, что частица находится в окрестности точки (x,y,z), среднее значение координаты 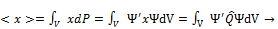в качестве оператора координаты выбираем .

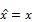2. Оператор импульса найдём исходя из соотношений неопределённости Гейзенберга: 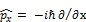, задача на собственные значения функции 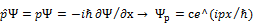. 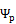-собственная функция, отвечающая за собственное значение импульса. Таким образом, собственная функция оператора импульса частицы с энергией и импульсом, сопоставляет волну частоты 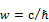и волновым числом .

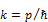3. Оператор Гамильтона (полной механической энергии) получается в соответствии с принципом классической механики из выражения для полной механической энергии с заменой физических величин их операторами. Оператор Гамильтона – оператор определяющий левую сторону УШ.

Условие одновременной измеримости различных физических переменных. Соотношение неопределённостей.

Рассмотрим условия, при которых А и В могут быть одновременно измерены. Пусть в некотором состоянии они имеют определённые значения, тогда их собственные операторы: 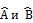: 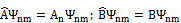. Предположим, что 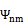образуют полную систему собственных векторов, тогда для произвольного вектора состояния: 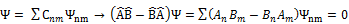. В силу произвольности 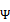получаем операторное равенство: 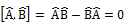. Другими словами, наблюдаемые должны коммутировать.

Соотношение неопределённостей Гейзенберга ( 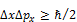) показывает, что между точностью, с которой одновременно может быть установлено положение частицы, и точностью её импульса существует определённое соотношение. (Соотношение неопределённостей Гейзенберга помогает определить вероятность нахождения частицы в данной точке пространства.)

Оператор момента импульса.

Момент импульса: 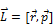, оператор момента импульса: 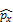=- 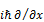. Компоненты оператора момента импульса: 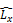=- 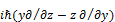. Вследствие коммутативности оператора, частица не может иметь определённые значения 2х, 3х компонентов момента импульса, при этом можно одновременно измерить и получить определённые значения квадрата момента импульса.

Перейдя к полярным координатам мы получим: 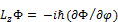, где 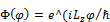). В силу стандартных условий проекция момента импульса может принимать только дискретный набор значений (Lz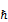=m , m= 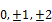…). Квадрат момента импульса: 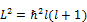, l= … .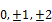

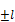infopedia.su